
分析 ①根据a>b>c,a+b+c=0,通过正、负来判断;
②根据对称轴列式得:a=b,与已知的a>b>c矛盾;
③由图象一定经过(1,0),且开口向上,得当x>1时,y>0;
④根据数形结合,利用抛物线与x轴的交点及与一元二次不等式的关系得出结论;
⑤分两种情况讨论,将x=2和x=-2代入可得结论.
解答  解:①∵a>b>c,a+b+c=0,
解:①∵a>b>c,a+b+c=0,
∴a、b、c中有正、负,
∵c为最小,a为最大,
∴c<0,a>0,
∴ac<0,
选项①正确;
②∵a+b+c=0,
∴图象一定经过(1,0),
对于二次函数,当x=-$\frac{b}{2a}$时,有最小值,
即-$\frac{b}{2a}$=-$\frac{1}{2}$,
∴a=b,
∵a>b>c,
所以选项②不正确;
③∵图象一定经过(1,0),且开口向上,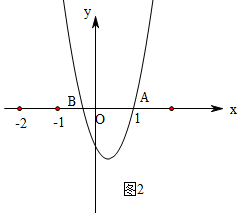
∴当x>1时,y>0,
所以③不正确;
④如图所示,设抛物线与x轴的交点为A(1,0),B(x1,0),
分两种情况:
i)当a>0,b>0,c<0时,抛物线对称轴在y轴的左侧,如图1,
∵a+b+c=0,
∴a+b=-c,
当x=-1时,y=a-b+c=a-b-a-b=-2b<0,
当x=-2时,y=4a-2b+c=4a-2b-a-b=3a-3b=3(a-b),
∵a>b,
∴a-b>0,
∴y>0,
∵A(1,0),
∴AB<3,
∴当满足am2+bm+c<0时,即当x=m时,y<0,
此时-2<m<1,
∴m+3>1,
则当x=m+3时,y>0,
∴a(m+3)2+b(m+3)+c>0,
ii)当a>0,b<0,c<0,抛物线对称轴在y轴的右侧,如图2,
∴a=-b-c,
当x=-1时,y=a-b+c=-b-c-b+c=-2b>0,
∴AB<2,
∴当am2+bm+c<0时,即当x=m时,y<0,
此时-1<m<1,
∴m+3>1,
则当x=m+3时,y>0,
∴a(m+3)2+b(m+3)+c>0,
所以④正确;
⑤当b>0时,x=-2时,y=4a-2b+c,
由④分析得:x>-2,
∴x=-2时,y>0,
∴正确;
当b>0时,4a-2|b|+c=4a+2b+c,
即x=2时,y=4a+2b+c>0,
所以⑤正确;
所以正确的命题序号是:①④⑤;
故答案为:①④⑤.
点评 本题考查了二次函数图象和系数的关系,利用数形结合的思想,本题有难度,同时与一元二次方程根与系数的关系相结合,熟练掌握二次函数的性质.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
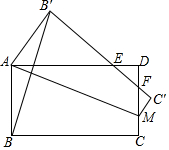 如图,长方形ABCD中,M为线段CD上一点,将四边形ABCM沿直线AM向上翻折使得点B、C分别落在点B′、C′处,线段B′C′分别交线段AD、CD于点E、F,连接BB′,若∠B′AE+∠BAM=∠AMC,且S△ABB′=2$\sqrt{2}$,则点B′到直线BC的距离为1+$\sqrt{2}$.
如图,长方形ABCD中,M为线段CD上一点,将四边形ABCM沿直线AM向上翻折使得点B、C分别落在点B′、C′处,线段B′C′分别交线段AD、CD于点E、F,连接BB′,若∠B′AE+∠BAM=∠AMC,且S△ABB′=2$\sqrt{2}$,则点B′到直线BC的距离为1+$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{41}{9}$ | B. | $\frac{41}{8}$ | C. | $\frac{41}{6}$ | D. | $\frac{41}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
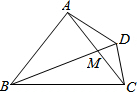 如图,在四边形ABCD中,∠BAC=∠BDC=90°,AB=AC=$\sqrt{5}$,CD=1,对角线的交点为M,则DM=$\frac{1}{2}$.
如图,在四边形ABCD中,∠BAC=∠BDC=90°,AB=AC=$\sqrt{5}$,CD=1,对角线的交点为M,则DM=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com