
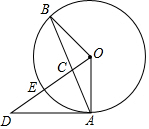
 如图,A、B是⊙O上的两点,过O作OB的垂线交AB于C,交⊙O于E,交⊙O的切线AD于D.
如图,A、B是⊙O上的两点,过O作OB的垂线交AB于C,交⊙O于E,交⊙O的切线AD于D.分析 (1)要证明DA=DC,只要证明∠ACD=∠CAD即可,根据题目中的条件可以得到∠ACD=∠CAD,结论得以证明;
(2)根据(1)中的结论和勾股定理可以求得DA及DE的长.
解答 (1)证明:∵OB⊥OC,OA⊥AD,
∴∠BOC=90°,∠OAD=90°,
∴∠BCO+∠OBC=∠OAC+∠CAD=90°,
∵OB=OA,
∴∠OBC=∠OAC,
∴∠BCO=∠CAD,
∵∠BCO=∠ACD,
∴∠ACD=∠CAD,
∴DA=DC;
(2)解:∵OA=5,OC=1,∠OAD=90°,DA=DC,
∴设DA=x,
则52+x2=(x+1)2,
解得,x=12,
∴DA=12,OD=13,
∵OE=OA,
∴OE=5,
∴DE=OD-OC=13-5=8.
点评 本题考查切线的性质,解答此类题目的关键是明确题目中所要证明的结论和所要解答的问题,然后根据数形结合和勾股定理的相关知识解答.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
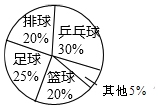 如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )| A. | 该班喜欢乒乓球的学生最多 | |
| B. | 该班喜欢排球和篮球的学生一样多 | |
| C. | 该班喜欢足球的人数是喜欢排球人数的1.25倍 | |
| D. | 该班喜欢其他球类活动的人数为5人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com