
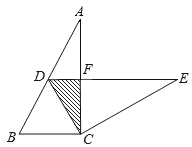
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2;将△ABC绕点顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,求n的大小和图中阴影部分的面积.
【答案】![]()
【解析】
由旋转的性质,易得BC=DC=2,由在Rt△ABC中,∠ACB=90°,∠A=30°,即可求得∠B=60°,即可判定△DBC是等边三角形,即可求得旋转角n的度数,易得△DFC是含30°角的直角三角形,则可求得DF与FC的长,继而求得阴影部分的面积.
解:∵将△ABC绕点C按顺时针方向旋转n度后得到△EDC,
∴BC=DC,
∵在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=90°﹣∠A=60°,
∴△DBC是等边三角形,
∴n=∠DCB=60°,
∴∠DCA=90°﹣∠DCB=90°﹣60°=30°,
∵BC=2,
∴DC=2,
∵∠FDC=∠B=60°,
∴∠DFC=90°,
∴![]()
∴![]()
∴S阴影=S△DFC![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
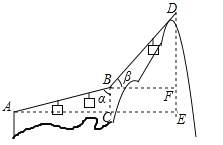
【题目】(2017安徽省)如图,游客在点A处做缆车出发,沿A﹣B﹣D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600m,α=75°,β=45°,求DE的长.
(参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
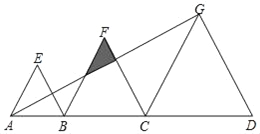
【题目】如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
①CD=____;
②图中阴影部分面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
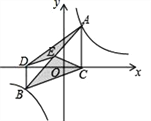
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
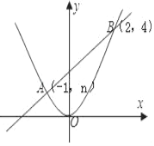
【题目】如图,一次函数y1=kx+b与二次函数y2=ax2的图象交于A(﹣1,n),B(2,4)两点.
(1)利用图中条件,求两个函数的解析式;
(2)根据图象直接写出使y1<y2的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家步行到校车站台,等候坐校车去学校,图中的折线表示这一过程中小明的路程S(km)与所花时间t(min)间的函数关系;下列说法:①他步行了1km到校车站台;②他步行的速度是100m/min;③他在校车站台等了6min;④校车运行的速度是200m/min;其中正确的个数是( )个.
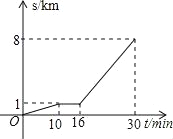
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 在
在![]() 上,弦
上,弦![]() ,垂足
,垂足![]() ,弦
,弦![]() ,垂足为
,垂足为![]() ,弦
,弦![]() 与
与![]() 相交于点
相交于点![]() ;
;
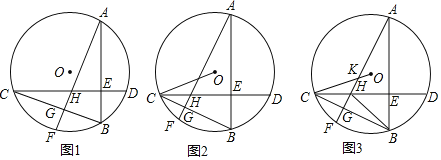
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求证:弧
时,求证:弧![]() 弧
弧![]() ;
;
(3)如图![]() ,在(2)的条件下,半径
,在(2)的条件下,半径![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com