
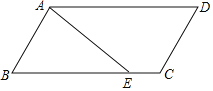
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是折线
是折线![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() 重合).则
重合).则![]() 的面积的最大值是( )
的面积的最大值是( )
A.![]() B.1C.
B.1C.![]() D.
D.![]()
【答案】D
【解析】
分三种情况讨论:①当点E在BC上时,高一定,底边BE最大时面积最大;②当E在CD上时,△ABE的面积不变;③当E在AD上时,E与D重合时,△ABE的面积最大,根据三角形的面积公式可得结论.
解:分三种情况:
①当点E在BC上时,E与C重合时,△ABE的面积最大,如图1,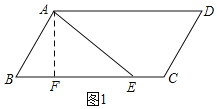
过A作AF⊥BC于F,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠C+∠B=180°,
∵∠C=120°,
∴∠B=60°,
Rt△ABF中,∠BAF=30°,
∴BF=![]() AB=1,AF=
AB=1,AF=![]() ,
,
∴此时△ABE的最大面积为:![]() ×4×
×4×![]() =2
=2![]() ;
;
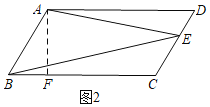
②当E在CD上时,如图2,此时,△ABE的面积=![]() SABCD=
SABCD=![]() ×4×
×4×![]() =2
=2![]() ;
;
③当E在AD上时,E与D重合时,△ABE的面积最大,此时,△ABE的面积=2![]() ,
,
综上,△ABE的面积的最大值是2![]() ;
;
故选:D.


科目:初中数学 来源: 题型:
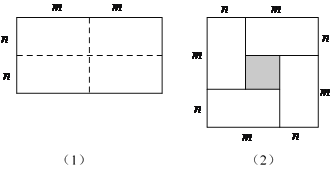
【题目】如图(1)是一个长为2m,宽为2n的长方形,沿图中虚线剪成四个均匀的小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少?
(2)观察图(2),你能写出下列三个代数式之间的等量关系吗?代数式:![]() ,
,![]() ,
,![]() ;
;
(3)已知:![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
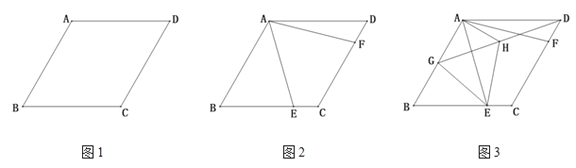
【题目】如图,在菱形ABCD中,∠ABC+∠ADC=120°,将一透明三角板60°角的顶点落在点A上,并绕着点A旋转,三角板的两边分别交BC、CD于点E、F.
(1)如图1,求∠BAD的度数;
(2)如图2,求证:BE+DF=AB;
(3)如图3,在(2)的条件下,取AB中点G,作等边△EGH,连接AH,延长GH刚好与平行四边形ABCD交于点D,若AH⊥AB,△EGH的面积为![]() .求DH的长.
.求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
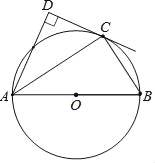
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
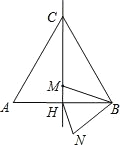
【题目】如图,在边长为 2a 的等边△ABC 中,M 是高 CH 所在直线上的一个动点, 连接 BM,将线段 BM 绕点 B 逆时针旋转 60°得到 BN,连接 HN,则在点 M 运动的过程中,线段 BN 长度的最小值为___________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.
(1) 采用树形图法(或列表法)列出两次摸球出现的所有可能结果;
(2) 求摸出的两个球号码之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区积极创建环保示范社区,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知温馨提示牌的单价为每个30元,垃圾箱的单价为每个90元,共需购买温馨提示牌和垃圾箱共100个.
(1)若规定温馨提示牌和垃圾箱的个数之比为1:4,求所需的购买费用;
(2)若该小区至多安放48个温馨提示牌,且费用不超过6300元,请列举所有购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年2月16日,由著名导演林超贤的电影《红海行动》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定谁去看电影,规则如下:在一个不透明的袋子中装有编号1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出两数和的所有可能的结果;
(2)分别求出小亮和小丽获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com