
 如图所示,已知点E是矩形ABCD边上一动点,沿A→D→C→B的路径移动,设点E经过的路径长为x,△ABE的面积是y,则下列能大致反映y与x的函数关系的图象是( )
如图所示,已知点E是矩形ABCD边上一动点,沿A→D→C→B的路径移动,设点E经过的路径长为x,△ABE的面积是y,则下列能大致反映y与x的函数关系的图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 随着E点的运动,△ABE的形状也在变化,依据点E的位置不同分三种情况考虑,从而得出结论.
解答 解:①当E点在线段AD上时,
△ABE的面积y=$\frac{1}{2}$AB•AE=$\frac{AB}{2}$x.
②当点E在线段CD上时,如图1,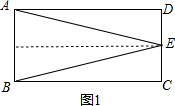
过E点作底AB边上的高,会发现高h=AD.
此时△ABE的面积y=$\frac{1}{2}$AB•AD与x无关,是固定的值.
③当点E运动到BC上时,如图2,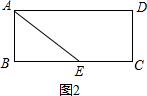
BE=AD+CD+BC-x,
此时△ABE的面积y=$\frac{1}{2}$AB•BE=$\frac{1}{2}$AB•(AD+CD+BC-x)=-$\frac{1}{2}$AB+$\frac{1}{2}$AB•(AD+CD+BC).
综合①②③可知,y关于x的函数图形为C.
故选C.
点评 本题考查了动点问题的函数图象,解题的关键是依据点E的位置不同分三种情况考虑.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | m=n | B. | m>n | C. | m<n | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,A、B为公路l同旁的两个村庄,在l上找一点P.
如图所示,A、B为公路l同旁的两个村庄,在l上找一点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com