
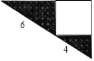
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
【答案】C
【解析】
先根据相似三角形的判定定理得出△AMB∽△CBE,故可得出![]() =
=![]() 的值,设CE=x,则BC=2x,在Rt△CBE中根据勾股定理求出x的值,故可得出CE,AB=BC,AM=2AB的值,再根据S草皮=S△CBE+S△AMB,即可得出结论.
的值,设CE=x,则BC=2x,在Rt△CBE中根据勾股定理求出x的值,故可得出CE,AB=BC,AM=2AB的值,再根据S草皮=S△CBE+S△AMB,即可得出结论.
解:∵△MDE是直角三角形,四边形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴![]() =
=![]() ,
,
∵MB=6,BE=4,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∵AB=BC,
∴![]() =
=![]() ,
,
设CE=2x,则BC=3x,在Rt△CBE中,BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=![]() ,
,
∴CE=![]() ,AB=BC=
,AB=BC=![]() ,AM=
,AM=![]() AB=
AB=![]() ,
,
∴S草皮=S△CBE+S△AMB=![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() =12.
=12.
故选:C.


科目:初中数学 来源: 题型:
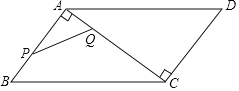
【题目】如图,在ABCD中,AB=6,BC=10,AB⊥AC,点P从点B出发沿着B→A→C的路径运动,同时点Q从点A出发沿着A→C→D的路径以相同的速度运动,当点P到达点C时,点Q随之停止运动,设点P运动的路程为x,y=PQ2,下列图象中大致反映y与x之间的函数关系的是( )
A. 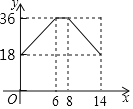 B.
B. 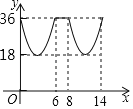
C. 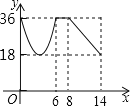 D.
D. 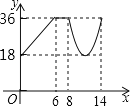
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
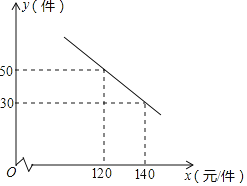
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某海上观测点B处观测到位于北偏东30°方向有一艘救船A,搜救船A最大航速50海里/时,AB=52![]() 海里,在位于观测点B的正东方向,搜救船A的东南方向有一失事渔船C,由于当天正值东南风,失事渔船C以2海里/时的速度向西北方向漂移,若不考虑大风对搜救船A的航线和航速的影响,求失事渔船获救的最快时间.
海里,在位于观测点B的正东方向,搜救船A的东南方向有一失事渔船C,由于当天正值东南风,失事渔船C以2海里/时的速度向西北方向漂移,若不考虑大风对搜救船A的航线和航速的影响,求失事渔船获救的最快时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=7+2![]() ,圆形纸片的半径为2,求圆心O运动的路径长为_____.
,圆形纸片的半径为2,求圆心O运动的路径长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束. 在整个运动过程中,点C运动的路程是( )
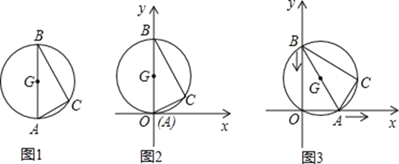
A. 4 B. 6 C. 4![]() ﹣2 D. 10﹣4
﹣2 D. 10﹣4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=9x2﹣6ax+a2﹣b
(1)当b=﹣3时,二次函数的图象经过点(﹣1,4)
①求a的值;
②求当a≤x≤b时,一次函数y=ax+b的最大值及最小值;
(2)若a≥3,b﹣1=2a,函数y=9x2﹣6ax+a2﹣b在﹣![]() <x<c时的值恒大于或等于0,求实数c的取值范围.
<x<c时的值恒大于或等于0,求实数c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com