练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】标有，，，，，六个数字的立方体的表面展开图如图所示，掷这个立方体一次，记朝上一面的数为，朝下一面的数为，得到平面直角坐标系中的一个点．已知小华前二次掷得的两个点所确定的直线经过点，则他第三次掷得的点也在这条直线上的概率为________．

    【答案】

    【解析】

    根据一次函数的性质，找出符合在这条直线上的点的个数，即可根据概率公式求解.

    每掷一次可能得到6个点的坐标分别是(其中有两个点是重合的)：

    (1,1),(1,1),(2,3),(3,2),(3,5),(5,3)，通过描点和计算可以发现，经过(1,1),(2,3),(3,5)，三点中的任意两点所确定的直线都经过点P(0,－1)，所以小华第三次掷得的点也在直线上的概率是，故答案为..

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛，某学校组织了一次体育知识竞赛．每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级得分依次记为100分、90分、80分、70分．学校将八年级一班和二班的成绩整理并绘制成统计图，如图所示．

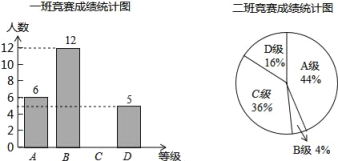
    （1）把一班竞赛成绩统计图补充完整；

    （2）写出下表中a、b、c的值：

    平均数（分）

    中位数（分）

    众数（分）

    方差

    一班

    a

    b

    90

    106.24

    二班

    87.6

    80

    c

    138.24

    （3）根据（2）的结果，请你对这次竞赛成绩的结果进行分析．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

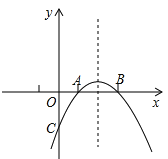
    【题目】已知：如图所示，抛物线y=-x2+bx+c与x轴的两个交点分别为A（1，0），B（3，0）．

    （1）求抛物线的解析式；

    （2）设点P在该抛物线上滑动，且满足条件S△PAB=1的点P有几个？并求出所有点P的坐标；

    （3）设抛物线交y轴于点C，问该抛物线对称轴上是否存在点M，使得△MAC的周长最小？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时,则∠MPN的度数为（ ）

    A. 140° B. 100° C. 50° D. 40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（12分）如图，矩形ABCD，AB＝6cm，AD＝2cm，点P以2cm/s的速度从顶点A出发沿折线A－B－C向点C运动，同时点Q以lcm/s的速度从顶点C出发向点D运动，当其中一个动点到达末端停止运动时，另一点也停止运动．

    (1)问两动点运动几秒，使四边形PBCQ的面积是矩形ABCD面积的；

    (2)问两动点经过多长时间使得点P与点Q之间的距离为？若存在，

    求出运动所需的时间；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一只不透明的袋子中装有个白球和个红球，这些球除颜色外都相同．

    搅匀后，从中任意摸出一个球，恰好是红球的概率是________；

    搅匀后，从中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出一个球．

    ①求两次都摸到红球的概率；②经过了次“摸球-记录-放回”的过程，全部摸到红球的概率是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：(1)2x2－x－2=0（配方法） (2)5－4x－12＝0（用求根公式）

    （3） （4）2（x－3）2 =x（x－3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数的图象如图，下列结论正确的序号是________

    ①；②；③当时，；④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=5，AD=a（a＞5）.点P在以A为圆心、AB长为半径的⊙A上，且在矩形ABCD的内部，P到AD、CD的距离PE、PF相等.

    （1）若a =7，求AE长；

    （2）若⊙A上满足条件的点P只有一个，求a的值；

    （3）若⊙A上满足条件的点P有两个，求a的取值范围．

    查看答案和解析>>

    同步练习册答案