已知二次函数y=2x2-(m+1)x+m-1.
(1)求证:无论m为何值,函数y的图象与x轴总有交点.并指出当m为何值时,函数y的图象与x轴只有一个交点?
(2)当m为何值时,函数y的图象过原点?并求出此时图象与x轴的另一交点的坐标;
(3)如果函数y的图象的顶点在第四象限,求m的取值范围.
【答案】
分析:(1)根据△=b
2-4ac的符号求出无论m为何值,函数y的图象与x轴总有交点,进而得出m=3时,函数y的图象与x轴只有一个交点;
(2)当函数图象过原点时,m
2-1=0,即可求出m的值,进而可求出抛物线的解析式,然后根据抛物线的解析式即可得出二次函数与x轴的另一交点的坐标;
(3)先用配方法求出二次函数的顶点坐标,然后让纵坐标大于0,纵坐标小于0即可求出m的取值范围.
解答:解:(1)
△=b
2-4ac,
=[-(m+1)]
2-4×2×(m-1),
=(m-3)
2≥0,
故无论m为何值,函数y的图象与x轴总有交点,
当m=3时,(m-3)
2=0,
即△=0,故函数y的图象与x轴只有一个交点;
(2)当图象过原点即图象过(0,0)点;故0=m-1,
解得:m=1,
当m=1时,函数y的图象过原点,
故此函数解析式为;y=2x
2-2x=2x(x-1),
当y=0,0=2x(x-1),
解得:x=0或1,
则图象与x轴的另一交点的坐标为(1,0);
(3)∵y=2x
2-(m+1)x+m-1,
=2(x
2-
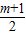
x)+m-1,
=2[(x-
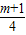
)
2-(
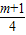
)
2]+m-1,
=2(x-
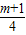
)
2-
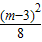
,
∴图象的顶点坐标为:(
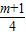
,-

),
∵函数y的图象的顶点在第四象限,
∴
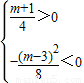
,
解得;m>-1且m≠3,
故m的取值范围为m>-1且m≠3.
点评:此题主要考查了二次函数的性质等知识点,将二次函数的解析式化为顶点式进行求解是解题的基本思路

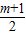 x)+m-1,
x)+m-1,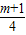 )2-(
)2-(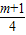 )2]+m-1,
)2]+m-1,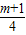 )2-
)2-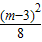 ,
,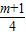 ,-
,- ),
),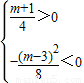 ,
,
