
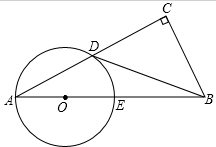
 如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.分析 (1)连接OD,如图,利用∠A=∠1和∠A+∠CDB=90°可得到∠1+∠CDB=90°,则∠BDO=90°,然后根据切线的判定定理可得到结论;
(2)连接DE,如图,设AD=a,则CD=x,利用圆周角定理得到∠ADE=90°,则DE∥AB,再证明∠CDB=∠ABC判定△CDB∽△CBA,利用相似比可计算出BC=$\sqrt{2}$a,接着利用勾股定理分别计算出BD=$\sqrt{3}$a,AB=$\sqrt{6}$a,则OD=$\frac{\sqrt{6}}{4}$a,然后在Rt△BOD中利用正切的定义求解.
解答 (1)证明:连接OD,如图,
∵OA=OD,
∴∠A=∠1,
∵∠A+∠CDB=90°,
∴∠1+∠CDB=90°,
∴∠BDO=90°,
∴OD⊥BD,
∴BD与⊙O相切;
(2)解:连接DE,如图, 设AD=a,则CD=x,
设AD=a,则CD=x,
∵AE为直径,
∴∠ADE=90°,
而∠C=90°,
∴DE∥AB,
∴∠AED=∠ABC,AE=BE,
∵∠A+∠CDB=90°,
∵∠A+∠AED=90°,
∴∠CDB=∠ABC,
∴△CDB∽△CBA,
∴CD:BC=BC:CA,即a:BC=BC:2a,
∴BC=$\sqrt{2}$a,
在Rt△CDB中,BD=$\sqrt{{a}^{2}+(\sqrt{2}a)^{2}}$=$\sqrt{3}$a,
在Rt△ABC中,AB=$\sqrt{(2a)^{2}+(\sqrt{2}a)^{2}}$=$\sqrt{6}$a,
∴AE=$\frac{\sqrt{6}}{2}$a,
∴OD=$\frac{\sqrt{6}}{4}$a,
在Rt△BOD中,tan∠DBO=$\frac{OD}{BD}$=$\frac{\frac{\sqrt{6}a}{4}}{\sqrt{3}a}$=$\frac{\sqrt{2}}{4}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了相似三角形的判定与性质.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查华为手机的使用寿命 | |
| B. | 调查市九年级学生的心理健康情况 | |
| C. | 调查你班学生打网络游戏的情况 | |
| D. | 调查中央电视台《中国舆论场》的节目收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.2×10-7米 | B. | 1.2×10-8米 | C. | 12×10-8米 | D. | 12×10-9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
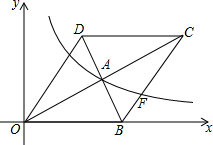 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是(6,$\frac{4}{3}$).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是(6,$\frac{4}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com