
分析 (1)根据0.$\stackrel{•}{7}$转化分数的方法,设 0.$\stackrel{•}{4}$=x,仿照例题的解法即可得出结论;
(2)①根据0.$\stackrel{•}{7}$转化分数的方法,设0.$\stackrel{•}{7}$$\stackrel{•}{3}$=x,仿照例题的解法(×10换成×100)即可得出结论;
②根据0.$\stackrel{•}{7}$转化分数的方法,设0.43$\stackrel{•}{2}$=x,仿照例题的解法即可得出结论.
解答 解:(1)设0.$\stackrel{•}{4}$=x.
方程两边都乘以10,可得10×0.$\stackrel{•}{4}$=10x.
由0.$\stackrel{•}{4}$=0.444…,可知10×0.$\stackrel{•}{4}$=4.444…=4+0.$\stackrel{•}{4}$,
即4+x=10x.
解得:x=$\frac{4}{9}$,即0.$\stackrel{•}{4}$=$\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
(2)①设0.$\stackrel{•}{7}$$\stackrel{•}{3}$=x.
方程两边都乘以100,可得100×0.$\stackrel{•}{7}$$\stackrel{•}{3}$=100x.
由0.$\stackrel{•}{7}$$\stackrel{•}{3}$=0.7373…,可知100×0.$\stackrel{•}{7}$$\stackrel{•}{3}$=73.7373…=73+0.$\stackrel{•}{7}$$\stackrel{•}{3}$,
即73+x=100x.
解得:x=$\frac{73}{99}$,即0.$\stackrel{•}{7}$$\stackrel{•}{3}$=$\frac{73}{99}$.
②设0.43$\stackrel{•}{2}$=x.
方程两边都乘以10,可得10×0.43$\stackrel{•}{2}$=10x.
由0.43$\stackrel{•}{2}$=0.43222…,可知10×0.43$\stackrel{•}{2}$=4.3222…=3.89+0.43$\stackrel{•}{2}$,
即3.89+x=10x.
解得:x=$\frac{389}{900}$,即0.43$\stackrel{•}{2}$=$\frac{389}{900}$.
点评 本题考查了一元一次方程的应用,读懂题意,能够仿照例题将循环小数转化为分数是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
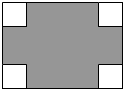 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量x(千克) | 销售价c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
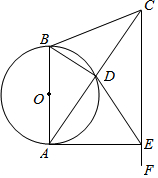 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com