
【题目】如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1 , △AEN的周长为C2 , 若 ![]() =
= ![]() ,求m的值;
,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+ ![]() E′B的最小值.
E′B的最小值.
【答案】
(1)
解:令y=0,则ax2+(a+3)x+3=0,
∴(x+1)(ax+3)=0,
∴x=﹣1或﹣ ![]() ,
,
∵抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),
∴﹣ ![]() =4,
=4,
∴a=﹣ ![]() .
.
∵A(4,0),B(0,3),
设直线AB解析式为y=kx+b,则 ![]() ,
,
解得 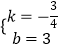 ,
,
∴直线AB解析式为y=﹣ ![]() x+3
x+3
(2)
解:如图1中,

∵PM⊥AB,PE⊥OA,
∴∠PMN=∠AEN,∵∠PNM=∠ANE,
∴△PNM∽△ANE,
∴ ![]() =
= ![]() ,
,
∵NE∥OB,
∴ ![]() =
= ![]() ,
,
∴AN= ![]() (4﹣m),
(4﹣m),
∵抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+3,
x+3,
∴PN=﹣ ![]() m2+
m2+ ![]() m+3﹣(﹣
m+3﹣(﹣ ![]() m+3)=﹣
m+3)=﹣ ![]() m2+3m,
m2+3m,
∴  =
= ![]() ,
,
解得m=2.
(3)
解:如图2中,在y轴上 取一点M使得OM= ![]() ,
,

∵OE′=2,OMOB= ![]() ×3=4,
×3=4,
∴OE′2=OMOB,
∴ ![]() =
= ![]() ,∵∠BOE′=∠MOE′,
,∵∠BOE′=∠MOE′,
∴△MOE′∽△E′OB,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ME′= ![]() BE′,
BE′,
∴AE′+ ![]() BE′=AE′+E′M=AM′,
BE′=AE′+E′M=AM′,
此时AE′+ ![]() BE′最小,最小值=AM=
BE′最小,最小值=AM= ![]() =
= ![]()
![]()
【解析】(1)令y=0,求出抛物线与x轴交点,列出方程即可求出a,根据待定系数法可以确定直线AB解析式.(2)由△PNM∽△ANE,推出 ![]() =
= ![]() ,列出方程即可解决问题.(3)在y轴上 取一点M使得OM=
,列出方程即可解决问题.(3)在y轴上 取一点M使得OM= ![]() ,构造相似三角形,可以证明AM就是E′A+
,构造相似三角形,可以证明AM就是E′A+ ![]() E′B的最小值.本题考查相似三角形的判定和性质、待定系数法、最小值问题等知识,解题的关键是构造相似三角形,找到线段AM就是E′A+
E′B的最小值.本题考查相似三角形的判定和性质、待定系数法、最小值问题等知识,解题的关键是构造相似三角形,找到线段AM就是E′A+ ![]() E′B的最小值,属于中考压轴题.
E′B的最小值,属于中考压轴题.
【考点精析】利用二次函数的最值和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣ ![]() x+n同时经过A(0,3)、B(4,0).
x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
问题:如图1,已知EF为△ABC的中位线,M是边BC上一动点,连接AM交EF于点P,那么动点P为线段AM中点.
理由:∵线段EF为△ABC的中位线,∴EF∥BC,
由平行线分线段成比例得:动点P为线段AM中点.
由此你得到动点P的运动轨迹是: .
(2)知识应用:
如图2,已知EF为等边△ABC边AB、AC上的动点,连结EF;若AF=BE,且等边△ABC的边长为8,求线段EF中点Q的运动轨迹的长.
(3)拓展提高:
如图3,P为线段AB上一动点(点P不与点A、B重合),在线段AB的同侧分别作等边△APC和等边△PBD,连结AD、BC,交点为Q.
①求∠AQB的度数;
②若AB=6,求动点Q运动轨迹的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=8 ![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
①甲车提速后的速度是60千米/时;
②乙车的速度是96千米/时;
③乙车返回时y与x的函数关系式为y=﹣96x+384;
④甲车到达B市乙车已返回A市2小时10分钟.
其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为(![]() ,
,![]() ),请解决以下问题:
),请解决以下问题:
(1)甲比乙晚出发几小时?
(2)分别求出甲、乙二人的速度;
(3)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地,若丙经过![]() h与乙相遇.
h与乙相遇.
①设丙与M地的距离为S(km),行驶的时间为t(h),求S与t之间的函数关系式(不用写自变量的取值范围)
②丙与乙相遇后再用多少时间与甲相遇.

查看答案和解析>>
科目:初中数学 来源: 题型:
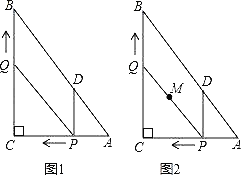
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
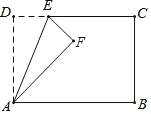
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com