
【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.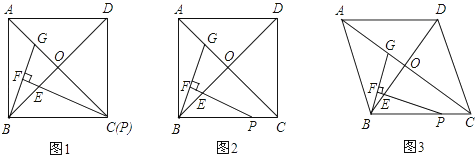
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)结合图②,通过观察、测量、猜想: ![]() 与
与 ![]() 的关系,并证明你的猜想;
的关系,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若AC=8,BD=6,直接写出 ![]() 的值.
的值.
【答案】
(1)证明:∵四边形ABCD是正方形,P与C重合,
∴OB=OP,∠BOC=∠BOG=90°,
∵PF⊥BG,∠PFB=90°,
∴∠GBO=90°﹣∠BGO,∠EPO=90°﹣∠BGO,
∴∠GBO=∠EPO,
在△BOG和△POE中, 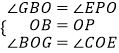
∴△BOG≌△POE(ASA);
(2)解:猜想 ![]() =
= ![]() .
.
证明:如图2,过P作PM∥AC交BG于M,交BO于N,
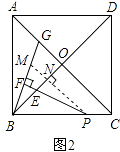
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB.
∴NB=NP.
∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中, 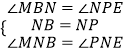
∴△BMN≌△PEN(ASA),
∴BM=PE.
∵∠BPE= ![]() ∠ACB,∠BPN=∠ACB,
∠ACB,∠BPN=∠ACB,
∴∠BPF=∠MPF.
∵PF⊥BM,
∴∠BFP=∠MFP=90°.
在△BPF和△MPF中, 
∴△BPF≌△MPF(ASA).
∴BF=MF.
即BF= ![]() BM.
BM.
∴BF= ![]() PE.
PE.
即 ![]() =
= ![]() ;
;
故答案为 ![]() ;
;
(3)解:如图3,
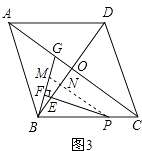
过P作PM∥AC交BG于点M,交BO于点N,
∴∠BPN=∠ACB=α,∠PNE=∠BOC=90°,
在Rt△BOC中,OC= ![]() AC=4,OB=
AC=4,OB= ![]() BD=3,
BD=3,
∴tan∠ACB= ![]() =
= ![]()
由(2)同理可得:BF= ![]() BM,∠MBN=∠EPN,
BM,∠MBN=∠EPN,
∵∠BNM=∠PNE=90°,
∴△BMN∽△PEN.
∴ ![]() .
.
在Rt△BNP中,tan∠ACB= ![]() =
= ![]() ,
,
∴ ![]() =tan∠ACB=
=tan∠ACB= ![]() .
.
即 ![]() =
= ![]() .
.
∴ ![]() =
= ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)先依据正方形的性质以及P与C重合,可证明OB=OP,∠BOC=∠BOG=90°,由同角的余角相等可得到∠GBO=∠EPO,然后依据ASA可得到△BOG≌△POE;
(2)过P作PM∥AC交BG于M,交BO于N,然后依据ASA可证明△BMN≌△PEN、△BPF≌△MPF(ASA),从而可得到BM=PE,BF=![]() BM.则可求得
BM.则可求得 ![]() 的值;
的值;
(3)过P作PM∥AC交BG于点M,交BO于点N,由(2)可知到BF=![]() ,∠MBN=∠EPN,然后再可证明△BMN∽△PEN,然后由相似三角形的对应边成比例求解即可.
,∠MBN=∠EPN,然后再可证明△BMN∽△PEN,然后由相似三角形的对应边成比例求解即可.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
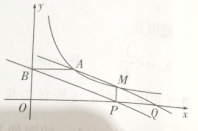
【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y=![]() (x>0)的图像上,
(x>0)的图像上,
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣ ![]() )2=
)2= ![]()
D.3x2﹣4x﹣2=0化为(x﹣ ![]() )2=
)2= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年10月31日,在广州举行的世界城市日全球主场活动开幕式上,住建部公布许昌成为“国家生态园林城市”在2018年植树节到来之际,许昌某中学购买了甲、乙两种树木用于绿化校园.若购买7棵甲种树和4棵乙种树需510元;购买3棵甲种树和5棵乙种树需350元.
(1)求甲种树和乙种树的单价;
(2)按学校规划,准备购买甲、乙两种树共200棵,且甲种树的数量不少于乙种树的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
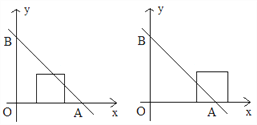
【题目】如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D。
(1)当点M在AB上运动时,四边形OCMD的周长为________;
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0<a≤4),在平移过程中:
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________;
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com