
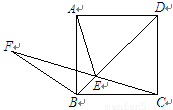
如图所示,在正方形ABCD的对角线上取点E,使得∠BAE= ,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE; ②F到BC的距离为
,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE; ②F到BC的距离为 ;③BE+EC=EF;④
;③BE+EC=EF;④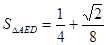 ;⑤
;⑤ .其中正确的个数是
.其中正确的个数是
A.2个 B.3个 C.4个 D.5个
B
【解析】
试题分析:根据正方形的性质推出AB=BC,∠ABD=∠CBD=45,证△ABE≌△CBE,即可判断①;过F作FH⊥BC于H,根据直角三角形的性质即可求出FH;过A作AM⊥BD交于M,根据勾股定理求出BD,根据三角形的面积公式即可求出高AM,根据三角形的面积公式求出即可.
∵正方形ABCD,
∴AB=BC,∠ABD=∠CBD=45°,
∵BE=BE,
∴△ABE≌△CBE,
∴AE=CE,∴①正确;
过F作FH⊥BC于H,

∵BF=BC=1,
∴∠BFC=∠FCB=15°,
∴FH= BF=
BF= ,∴②错误;
,∴②错误;
∵Rt△BHF中,FH= ,BF=1,
,BF=1,

∵BD是正方形ABCD的对角线,
∴AE=CE,
在EF上取一点N,使BN=BE,

又∠NBE=∠EBC+∠ECB=45°+15°=60°,
∴△NBE为等边三角形,
∴∠ENB=60°,又∠NFB=15°,
∴∠NBF=45°,又∠EBC=45°,
∴∠NBF=∠EBC,又BF=BC,∠NFB=∠ECB=15°,
可证△FBN≌△CBE,
∴NF=EC,
故BE+EC=EN+NF=EF,
∴③正确;
过A作AM⊥BD交于M,
根据勾股定理求出BD=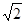 ,
,
由面积公式得:AD×AB=BD×AM,解得
∵∠ADB=45°,∠AED=60°,
∴ ,
,
∴ ,∴④错误;
,∴④错误;

故选B.
考点:正方形的性质,全等三角形的性质和判定,三角形的面积,勾股定理,含30°角的直角三角形的性质
点评:本题知识点多,综合性强,是中考常见题,综合运用这些性质进行证明是解此题的关键.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
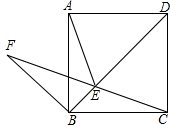 (2013•凤阳县模拟)如图所示,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为
(2013•凤阳县模拟)如图所示,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为
| ||
| 2 |
| 1 |
| 4 |
| ||
| 8 |
| ||
| 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
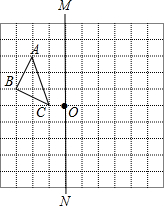 如图所示,在正方形网格上有一个△ABC.
如图所示,在正方形网格上有一个△ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com