
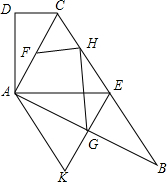
 如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.
如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.分析 (1)由已知条件易证△ACD∽△BCA,由相似三角形的性质可得∠CAD=∠CBA,再结合已知条件和直角三角形的性质证明∠DAE=90°即可;
(2)利用“在直角三角形中,30度角所对的直角边等于斜边的一半”、“直角三角形斜边上的中线等于斜边的一半”推知四边形AKEC的四条边都相等,则四边形AKEC是菱形.
解答 解:
(1)证明:∵AC2=CD•BC,
∴$\frac{CD}{AC}=\frac{AC}{BC}$,
∵AC平分∠BCD,
∴∠ACD=∠BCA,
∴△ACD∽△BCA,
∴∠CAD=∠CBA,
∵AC⊥AB,
∴∠CAB=90°,
∴∠CDA=90°,
在Rt△ABC中,∵E是BC的中点,
∴EA=EB=EC,
∴∠EAC=∠BCA=∠DCA,
∴AE∥CD,
∴∠DAE=180°-∠CDA=180°-90°=90°,
∴AD⊥AE;
(2)证明:
∵EK⊥AB,AC⊥AB,
∴EK∥AC,
又∵∠B=30°,
∴AC=$\frac{1}{2}$BC=EB=EC.
又∵EK=EB,
∴EK=AC,
即AK=KE=EC=CA,
∴四边形AKEC是菱形.
点评 本题考查了菱形的性质以及相似三角形的判定与性质,熟练掌握“直角三角形斜边上的中线等于斜边的一半”、“在直角三角形中,30度角所对的直角边等于斜边的一半”以及菱形的判定是解题的关键,此题难度较大.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
 在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.
在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
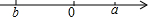 已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )
已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )| A. | a+b | B. | 3a-3b | C. | a-b | D. | a-3b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 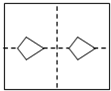 | C. | 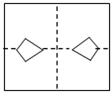 | D. | 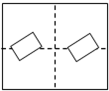 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 非负数一定是正数 | |
| B. | 有最小的正整数,有最小的正有理数 | |
| C. | 0既不是整数,也不是负数 | |
| D. | 正整数和正分值统称正有理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
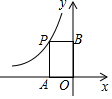 反比例函数y=-$\frac{3}{x}$(x<0)如图所示,则矩形OAPB的面积是( )
反比例函数y=-$\frac{3}{x}$(x<0)如图所示,则矩形OAPB的面积是( )| A. | 3 | B. | -3 | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com