
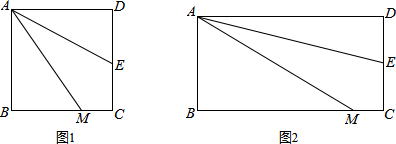
分析 (1)先构造出△ADE≌△NCE,即可得出结论;
(2)同(1)的方法即可得出结论;
(3)设出MC=x,利用(2)的结论得出AM=9+x,再利用勾股定理建立方程求出CM即可得出结论.
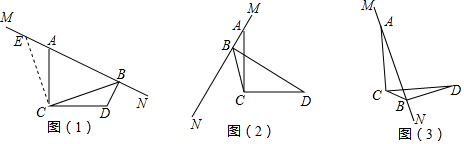
解答 解:(1)如图1,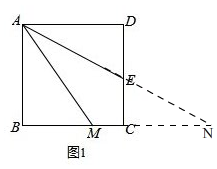 延长AE,BC相交于N,
延长AE,BC相交于N,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠∠DAE=∠MAE,
∴∠ENC=∠MAE,在△ADE和△NCE中,$\left\{\begin{array}{l}{∠DAE=∠CNE}\\{∠AED=∠NEC}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;
(2)结论AM=AD+CM仍然成立,
理由:如图2,
延长AE,BC相交于N,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
在△ADE和△NCE中,$\left\{\begin{array}{l}{∠DAE=∠CNE}\\{∠AED=∠NEC}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;
(3)设MC=x,则BM=BC-CN=9-x,
由(2)知,AM=AD+MC=9+x,
在Rt△ABC中,AM2-BM2=AB2,
(9+x)2-(9-x)2=36,
∴x=1,
∴AM=AD+MC=10.
点评 此题是四边形综合题,主要考查了正方形的性质,矩形的性质,全等三角形的判定和性质,勾股定理,解本题的关键是判断出△ADE≌△NCE和利用勾股定理建立方程,是一道基础题目.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
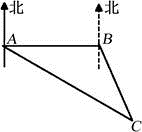
如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
查看答案和解析>>
科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列各数: 3.14159, 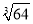 ,
, 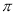 ,
, 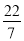 ,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有( )
,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
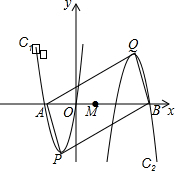 如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.
如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
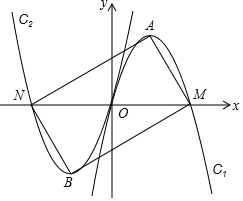 如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )
如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com