
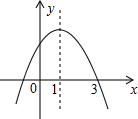 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,根据抛物线与x轴是否有交点确定b2-4ac的取值范围,根据对称轴x=-$\frac{b}{2a}$=1即可确定2a+b的取值范围,根据b=-2a,a<0可以确定a+b>0是否成立.
解答 解:∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=-$\frac{b}{2a}$,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道抛物线与x轴有两个交点,
∴b2-4ac>0,故②错误.
∵对称轴x=-$\frac{b}{2a}$=1,
∴b=-2a,
∴2a+b=0,故③正确;
∵b=-2a,
∴a+b=a-2a=-a,
∴a<0,
∴-a>0,
∴a+b>0,故④正确;
故选B.
点评 此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
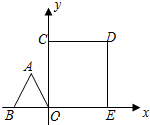 如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是11-2$\sqrt{3}$.
如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是11-2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com