
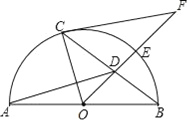
【题目】如图,AB是半圆O上的直径,E是![]() 的中点,OE交弦BC于点D,过点C作⊙O的切线交OE的延长线于点F,已知BC=8,DE=2.
的中点,OE交弦BC于点D,过点C作⊙O的切线交OE的延长线于点F,已知BC=8,DE=2.
(1)求⊙O的半径;
(2)求CF的长.
【答案】(1)⊙O的半径5;
(2)CF的长为![]() .
.
【解析】试题分析:
(1)根据垂径定理得△ODC是直角三角形,再用勾股定理列方程即可求出圆的半径;
(2)证△OCD∽△OFC,由相似三角形的对应边成比例求出OF的长,在Rt△OCF中,用勾股定理可求出CF的长.
试题解析:
(1)设⊙O的半径为x,
∵E点是![]() 的中点,O点是圆心,∴OD⊥BC,DC=
的中点,O点是圆心,∴OD⊥BC,DC=![]() =4,
=4,
在Rt△ODC中,OD=x﹣2,∴OD2+DC2=OC2
∴(x﹣2)2+42=x2
∴x=5,即⊙O的半径为5;
(2)∵FC是⊙O的切线,
∴OC⊥CF
又∵E是![]() 的中点.∴OD⊥BC,∴OC2=ODOF,即52=3OF
的中点.∴OD⊥BC,∴OC2=ODOF,即52=3OF
∴![]() ,在Rt△OCF中,OC2+CF2=OF2
,在Rt△OCF中,OC2+CF2=OF2
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为__.
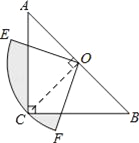
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
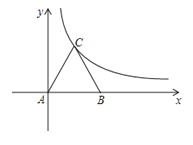
【题目】如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
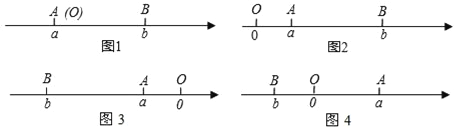
【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名学生军训时连续射靶10次,命中环数分别为 7,8,6,8,5,9,10,7,6,4.则这名学生射击环数的方差是( )
A. 3 B. 2.9 C. 2.8 D. 2.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com