
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.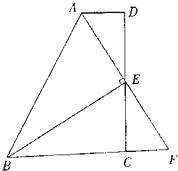
求证:
(1)FC=AD
(2)AB=BC+AD.
【答案】
(1)
解:(1)∵AD∥BC,∴∠ADC=∠ECF,∵E是CD的中点,∴DE=EF,∵在△ADE与△FCE中,∠ADC=∠ECF,DE=EF,∠AED=∠CEF,∴△ADE≌△FCE(ASA),∴FC=AD;
(2)
解:∵△ADE≌△FCE,∴AE=EF,AD=CF,又∵BE⊥AE,∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF,∵AD=CF,∴AB=BC+AD.
【解析】(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答;(2)根据线段垂直平分线的性质判断出AB=BF即可.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
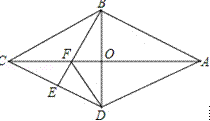
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
(1)证明:△CBF≌△CDF;
(2)若AC=2![]() ,BD=2,求四边形ABCD的周长。
,BD=2,求四边形ABCD的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
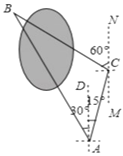
【题目】小明同学要测量公园内被湖水隔开的两颗大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°的方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米;参考数据![]() ,
, ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,分别以A、B为圆心,大于线段AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC,求∠ADC的度数. 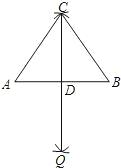
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣1,y1)、B(2,y2)、C(﹣3,y3)在函数y=﹣2(x+1)2+3的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3
B.y1<y3<y2
C.y2<y3<y1
D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC. 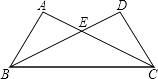
(1)求证:△ABE≌△DCE;
(2)当∠AEB=70°时,求∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com