
ЁОЬтФПЁПЗжРрЬжТлЪЧвЛжжЗЧГЃживЊЕФЪ§бЇЗНЗЈЃЌШчЙћвЛЕРЬтЬсЙЉЕФвбжЊЬѕМўжаАќКЌМИжжЧщПіЃЌЮвУЧПЩвдЗжЧщПіЬжТлРДЧѓНт.Р§ШчЃКвбжЊЕуAЃЌBЃЌCдквЛЬѕжБЯпЩЯЃЌШєAB=8ЃЌBC=3дђACГЄЮЊЖрЩйЃП
ЭЈЙ§ЗжЮіЮвУЧЗЂЯжЃЌТњзуЬтвтЕФЧщПігаСНжжЃКЧщПіЕБЕуCдкЕуBЕФгвВрЪБЃЌШчЭМ1ЃЌДЫЪБЃЌAC=11ЃЛ

ЧщПіЂкЕБЕуCдкЕуBЕФзѓВрЪБЃЌ ШчЭМ2ДЫЪБЃЌAC=5.

ЗТееЩЯУцЕФНтЬтЫМТЗЃЌЭъГЩЯТСаЮЪЬт:
ЮЪЬтЃЈ1ЃЉ: ШчЭМ,Ъ§жсЩЯЕуAКЭЕуBБэЪОЕФЪ§ЗжБ№ЪЧ-1КЭ2ЃЌЕуCЪЧЪ§жсЩЯвЛЕуЃЌЧвBC=2ABЃЌдђЕуCБэЪОЕФЪ§ЪЧ.
![]()
ЮЪЬт(2): Шє![]() ЃЌ
ЃЌ![]() Чѓ
Чѓ![]() ЕФжЕ.
ЕФжЕ.
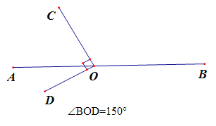
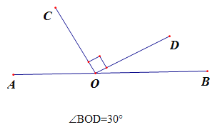
ЮЪЬт(3): ЕуOЪЧжБЯпABЩЯвЛЕуЃЌвдOЮЊЖЫЕузїЩфЯпOCЁЂODЃЌЪЙ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЈЛГіЭМаЮЃЌжБНгаДГіНсЙћЃЉ.
ЕФЖШЪ§ЃЈЛГіЭМаЮЃЌжБНгаДГіНсЙћЃЉ.
![]()
ЁОД№АИЁПЮЪЬтЃЈ1)ЕуCБэЪОЕФЪ§ЪЧ8Лђ-4ЃЛЮЪЬтЃЈ2ЃЉ![]() ЕФжЕЮЊ1ЃЌ-1ЃЌ5ЃЌ-5ЃЛЮЪЬтЃЈ3ЃЉ
ЕФжЕЮЊ1ЃЌ-1ЃЌ5ЃЌ-5ЃЛЮЪЬтЃЈ3ЃЉ![]() ,
, ![]() ЃЛМћНтЮі.
ЃЛМћНтЮі.
ЁОНтЮіЁП
ЮЪЬтЃЈ1)ЗжСНжжЧщПіНјааЬжТлЃЌЕБCдкBЕФзѓВрвдМАЕБCдкBЕФгвВрЃЌВЂвРОнBC=2ABНјааЗжЮіМЦЫу.
ЮЪЬтЃЈ2ЃЉРћгУ![]() ЃЌ
ЃЌ![]() ЕУЕН
ЕУЕН![]() ЃЌдйНјааЗжРрЬжТлДњШыxЃЌyЧѓжЕ.
ЃЌдйНјааЗжРрЬжТлДњШыxЃЌyЧѓжЕ.
ЮЪЬтЃЈ3ЃЉИљОнЬтвтЛГіЭМаЮЃЌРћгУНЧЕФКЭВюЙиЯЕНјааМЦЫуЃЌжБНгаДГіД№АИ.
НтЃКЮЪЬтЃЈ1) ЕуCЪЧЪ§жсЩЯвЛЕуЃЌЧвBC=2ABЃЌНсКЯЪ§жсПЩжЊЕБCдкBЕФзѓВрвдМАЕБCдкBЕФгвВрЗжБ№ЮЊ-4Лђ8.
ЮЪЬт(2ЃЉЁп![]() ЃЌ
ЃЌ![]() Ёр
Ёр![]()
ЧщПіЕБx=2ЃЌy=3ЪБЃЌ![]() =5ЃЌ
=5ЃЌ
ЧщПіЕБx=2ЃЌy=-3ЪБЃЌ![]() =-1ЃЌ
=-1ЃЌ
ЧщПіЂл ЕБx=-2ЃЌy=3ЪБЃЌ![]() =1ЃЌ
=1ЃЌ
ЧщПіЂм ЕБx=-2ЃЌy=-3ЪБЃЌ![]() =-5ЃЌ
=-5ЃЌ
ЫљвдЃЌ![]() ЕФжЕЮЊ1ЃЌ-1ЃЌ5ЃЌ-5.
ЕФжЕЮЊ1ЃЌ-1ЃЌ5ЃЌ-5.
ЮЪЬтЂЧ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЯТБэЃЌДгзѓЕНгвдкУПИіаЁИёжаЖМЬюШывЛИіећЪ§ЃЌЪЙЕУШЮвтШ§ИіЯрСкИёзгЫљЬюећЪ§жЎКЭЖМЯрЕШЃЌдђЕк2018ИіИёзгжаЕФећЪ§ЪЧ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
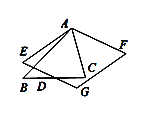
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯBACЃН60ЁуЃЌЁЯBЃН45ЁуЃЌABЃН2ЃЌЕуDЪЧBCЩЯЕФвЛИіЖЏЕуЃЌЕуDЙигкABЃЌACЕФЖдГЦЕуЗжБ№ЪЧЕуEЃЌFЃЌЫФБпаЮAEGFЪЧЦНааЫФБпаЮЃЌдђЫФБпаЮAEGFУцЛ§ЕФзюаЁжЕЪЧ ЃЈ ЃЉ
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫу
ЃЈ1ЃЉ5+ЃЈЉ6ЃЉ+3ЉЃЈЉ9ЃЉ+ЃЈЉ4ЃЉЉ7
ЃЈ2ЃЉЃЈЉ2ЃЉ2Љ8ЁТЃЈЉ2ЃЉЉ4ЁС|Љ5|
ЃЈ3ЃЉЉ22ЁТ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
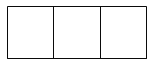
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЌНЋAЁЂBЁЂCШ§ИізжФИЫцЛњЬюаДдкШ§ИіПеИёжаЃЈУППеЬювЛИізжФИЃЌУППежаЕФзжФИВЛжиИДЃЉЃЌЧыФугУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓДгзѓЭљгвзжФИЫГађЧЁКУЪЧAЁЂBЁЂCЕФИХТЪЃЛ
ЃЈ2ЃЉШєдкШчЭМШ§ИіПеИёЕФгвВрдіМгвЛИіПеИёЃЌНЋAЁЂBЁЂCЁЂDЫФИізжФИШЮвтЬюаДЦфжаЃЈУППеЬювЛИізжФИЃЌУППежаЕФзжФИВЛжиИДЃЉЃЌДгзѓЭљгвзжФИЫГађЧЁКУЪЧAЁЂBЁЂCЁЂDЕФИХТЪЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭъГЩЯТУцЕФЭЦРэЙ§ГЬ.
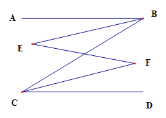
ШчЭМЃЌABЁЮCDЃЌBEЁЂCFЗжБ№ЪЧЁЯABCКЭЁЯBCDЕФЦНЗжЯп.ЧѓжЄЃКЁЯE=ЁЯF
жЄУїЃКЁпABЁЮCDЃЈвбжЊЃЉ
ЁрЁЯABC=ЁЯBCDЃЈ ЃЉ
ЁпBEЁЂCFЗжБ№ЪЧЁЯABCКЭЁЯBCDЕФЦНЗжЯпЃЈвбжЊЃЉ
ЁрЁЯCBE=![]() ЁЯABCЃЌЁЯBCF=
ЁЯABCЃЌЁЯBCF=![]() ЁЯBCDЃЈ ЃЉ
ЁЯBCDЃЈ ЃЉ
ЁрЁЯCBE=ЁЯBCFЃЈ ЃЉ
ЁрBEЁЮCFЃЈ ЃЉ
ЁрЁЯE=ЁЯF( )
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЖўДЮКЏЪ§y=ax2Љ2axЉ3aЃЈaЃМ0ЃЉЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФгвВрЃЉЃЌгыyжсЕФе§АыжсНЛгкЕуCЃЌЖЅЕуЮЊDЃЎ
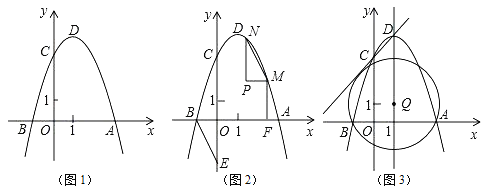
ЃЈ1ЃЉЧѓЖЅЕуDЕФзјБъЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЃЈ2ЃЉШєвдADЮЊжБОЖЕФдВОЙ§ЕуCЃЎ
ЂйЧѓaЕФжЕЃЎ
ЂкШчЭМ2ЃЌЕуEЪЧyжсИКАыжсЩЯвЛЕуЃЌСЌНгBEЃЌНЋЁїOBEШЦЦНУцФкФГвЛЕуа§зЊ180ЁуЃЌЕУЕНЁїPMNЃЈЕуPЁЂMЁЂNЗжБ№КЭЕуOЁЂBЁЂEЖдгІЃЉЃЌВЂЧвЕуMЁЂNЖМдкХзЮяЯпЩЯЃЌзїMFЁЭxжсгкЕуFЃЌШєЯпЖЮBF=2MFЃЌЧѓЕуMЁЂNЕФзјБъЃЎ
ЂлШчЭМ3ЃЌЕуQдкХзЮяЯпЕФЖдГЦжсЩЯЃЌвдQЮЊдВаФЕФдВЙ§AЁЂBСНЕуЃЌВЂЧвКЭжБЯпCDЯрЧаЃЌЧѓЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПтљШЛУРЪГЕъЕФAЁЂBСНжжВЫЦЗЃЌУПЗнГЩБООљЮЊ14дЊЃЌЪлМлЗжБ№ЮЊ20дЊЁЂ18дЊЃЌетСНжжВЫЦЗУПЬьЕФгЊвЕЖюЙВЮЊ1120дЊЃЌзмРћШѓЮЊ280дЊЃЎ
ЃЈ1ЃЉИУЕъУПЬьТєГіетСНжжВЫЦЗЙВЖрЩйЗнЃП
ЃЈ2ЃЉИУЕъЮЊСЫдіМгРћШѓЃЌзМБИНЕЕЭAжжВЫЦЗЕФЪлМлЃЌЭЌЪБЬсИпBжжВЫЦЗЕФЪлМлЃЌЪлТєЪБЗЂЯжЃЌAжжВЫЦЗЪлМлУПНЕ0.5дЊПЩЖрТє1ЗнЃЛBжжВЫЦЗЪлМлУПЬсИп0.5дЊОЭЩйТє1ЗнЃЌШчЙћетСНжжВЫЦЗУПЬьЯњЪлзмЗнЪ§ВЛБфЃЌФЧУДетСНжжВЫЦЗвЛЬьЕФзмРћШѓзюЖрЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊЙФРјЪаУёНкдМгУЫЎЃЌздРДЫЎЙЋЫОАДЗжЖЮЪеЗбБъзМЪеЗбЃЌШчЭМЗДгГЕФЪЧУПдТЫЎЗб![]() ЃЈдЊЃЉгыгУЫЎСП
ЃЈдЊЃЉгыгУЫЎСП![]() ЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕ.
ЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕ.
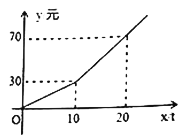
ЃЈ1ЃЉЕБгУЫЎСПГЌЙ§10ЖжЪБЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЈВЛБиаДздБфСПШЁжЕЗЖЮЇЃЉЃЛ
ЕФКЏЪ§НтЮіЪНЃЈВЛБиаДздБфСПШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉАДЩЯЪіЗжЖЮЪеЗбБъзМаЁДЯМвШ§ЁЂЫФдТЗнЗжБ№НЛЫЎЗб38дЊКЭ27дЊЃЌЮЪЫФдТЗнБШШ§дТЗнНкдМгУЫЎЖрЩйЖжЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com