
科目:初中数学 来源: 题型:填空题
 在数学课上,老师提出如下问题:已知:直线AB和直线AB外一点O.
在数学课上,老师提出如下问题:已知:直线AB和直线AB外一点O.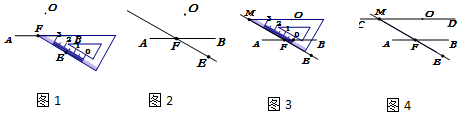
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
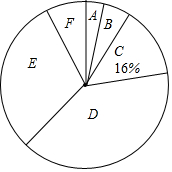 为了了解光明中学学生平均每周的体育锻炼时间,小敏在校内随机调查了50名同学,统计并绘制了频数分布表(如下表)和扇形统计图(如图).
为了了解光明中学学生平均每周的体育锻炼时间,小敏在校内随机调查了50名同学,统计并绘制了频数分布表(如下表)和扇形统计图(如图).| 组别 | 锻炼时间(h/周) | 频数 |
| A | 1.5≤t<3 | 1 |
| B | 3≤t<4.5 | 2 |
| C | 4.5≤t<6 | a |
| D | 6≤t<7.5 | 20 |
| E | 7.5≤t<9 | 15 |
| F | t≥9 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
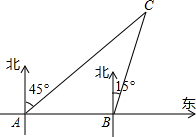 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com