Question

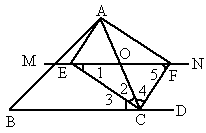
如图所示，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．

(1)试说明EO=FO；

(2)当点O运动到何处时，四边形AECF是矩形？请简要说明理由．

Answer 1

答案：
解析：

解：(1)因为CE平分∠ACB， 所以∠2=∠3． 又因为MN∥BC，所以∠1=∠3，所以∠1=∠2，所以OE=OC． 同理∠4=∠5，所以OC=OF，所以OE=OF． (2)当点O运动到AC的中点时，四边形AECF是矩形，如图所示证明如下：因为无论O在AC上怎样运动，都有OF=OE，所以四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)． 因为CE是∠ACB的平分线，CF是∠ACD的平分线， 所以，． 因为∠ACB＋∠ACD=180°， 所以∠1＋∠2=90°， 所以四边形AECF是矩形．

提示：

(1)因为MN∥BC，CE、CF分别是角平分线，所以∠CEO=∠ECO，∠CFO=∠FCO，所以OE=OC，FO=CO，所以EO=FO． (2)由(1)知EO=FO，当AO=CO时四边形AECF是平行四边形，由CE、CF分别平分∠ACB、∠ACD得∠ECF=90°，所以四边形AECF是矩形．