
【题目】如图,天星山山脚下西端A处与东端B处相距800(1+ ![]() )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 ![]() 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
【答案】解:过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,
∵∠A=45°,CD⊥AB,
∴AD=CD=x米,
∴AC= ![]() x.
x.
在Rt△BCD中,
∵∠B=30°,
∴BC= ![]() =
= ![]() =2x,
=2x,
∵小军的行走速度为 ![]() 米/秒.若小明与小军同时到达山顶C处,
米/秒.若小明与小军同时到达山顶C处,
∴ ![]() =
= ![]() ,解得a=1米/秒.
,解得a=1米/秒.
答:小明的行走速度是1米/秒.
【解析】过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,根据直角三角形的性质用x表示出AC与BC的长,再根据小明与小军同时到达山顶C处即可得出结论.本题考查的是解直角三角形的应用﹣坡度坡角问题,根据题意作出辅助线,利用锐角三角函数的定义求解是解答此题的关键.
【考点精析】通过灵活运用关于坡度坡角问题,掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】给出下列长度的四组线段:①1,![]() ,
,![]() ;②3,4,5;③6,7,8;④a2-1,a2+1,2a(a为大于1的正整数).其中能组成直角三角形的有( )
;②3,4,5;③6,7,8;④a2-1,a2+1,2a(a为大于1的正整数).其中能组成直角三角形的有( )
A.①②③B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、C分别在x轴上、y轴上,CB//OA,OA=8,若点B的坐标为(a,b),且b=![]() .
.
(1)直接写出点A、B、C的坐标;
(2)若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;
(3)在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①在同一平面内不相交的两条线段必平行
②过两条直线![]() 外一点
外一点![]() ,一定可做直线
,一定可做直线![]() ,使
,使![]() ,且
,且![]()
③过直线外一点有且只有一条直线与已知直线平行
④两直线被第三条直线所截得的同旁内角的平分线互相垂直
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
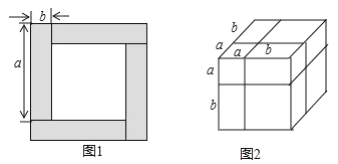
【题目】通常情况下,用两种不同的方法计算同一图形的面积,可以得到一个恒等式,
①如图1,根据图中阴影部分的面积可表示为__________,还可表示为___________,可以得到的恒等式是___________.
②类似地,用两种不同的方法计算同一各几何体的体积,也可以得到一个恒等式,如图2是边长为![]() 的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=-3x+3与x轴,y轴分别交于A,B,两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求k的值;
(2)若将正方形沿x轴负方向平移m个单位长度后,点C恰好落在该反比例函数的图象上,则m的值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
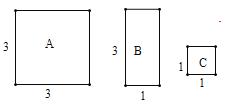
【题目】如图,有A、B、C三种不同型号的卡片,每种卡片各有9张.其中A型卡片是边长为3的正方形,B型卡片是相邻两边长分别为3、1的长方形,C型卡片是边长为1的正方形.从其中取若干张卡片(每种卡片至少取1张),若把取出的这些卡片拼成一个正方形,则所拼正方形的边长的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(3a-5,a+1)
(1)若点A在y轴上,求点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信支付、转账,把微信账户里的钱转到银行卡叫做提现,自2016年3月1日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为1800元,他需支付手续费_____元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下,问:小明3次提现金额共计多少元?
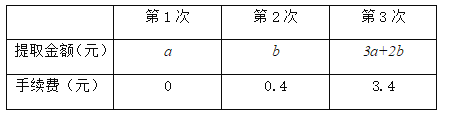
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com