
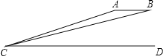
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.

(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】(1)由AB=AC知∠ABC=∠ACB,由等腰三角形三线合一知AM⊥BC,从而根据∠MAB+∠ABC=∠EBC+∠ACB知∠MAB=∠EBC,再由△MBN为等腰直角三角形知∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°可得证;
(2)设BM=CM=MN=a,知DN=BC=2a,证△ABN≌△DBN得AN=DN=2a,Rt△ABM中利用勾股定理可得a的值,从而得出答案;
(3)F是AB的中点知MF=AF=BF及∠FMN=∠MAB=∠CBD,再由![]() 即可得证.
即可得证.
(1)∵AB=AC,
∴∠ABC=∠ACB,
∵M为BC的中点,
∴AM⊥BC,
在Rt△ABM中,∠MAB+∠ABC=90°,
在Rt△CBE中,∠EBC+∠ACB=90°,
∴∠MAB=∠EBC,
又∵MB=MN,
∴△MBN为等腰直角三角形,
∴∠MNB=∠MBN=45°,
∴∠EBC+∠NBE=45°,∠MAB+∠ABN=∠MNB=45°,
∴∠NBE=∠ABN,即BN平分∠ABE;
(2)设BM=CM=MN=a,
∵四边形DNBC是平行四边形,
∴DN=BC=2a,
在△ABN和△DBN中,
∵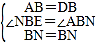 ,
,
∴△ABN≌△DBN(SAS),
∴AN=DN=2a,
在Rt△ABM中,由AM2+MB2=AB2可得(2a+a)2+a2=1,
解得:a=±![]() (负值舍去),
(负值舍去),
∴BC=2a=![]() ;
;
(3)∵F是AB的中点,
∴在Rt△MAB中,MF=AF=BF,
∴∠MAB=∠FMN,
又∵∠MAB=∠CBD,
∴∠FMN=∠CBD,
∵![]() ,
,
∴![]() ,
,
∴△MFN∽△BDC.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N.AH⊥MN于点H.
(1)当∠MAN绕点A旋转到BM=DN时,请你直接写出线段AH与AB的数量关系______.(不需证明)
(2)当∠MAN绕点A旋转到BM≠DN时,问(1)中线段AH与AB的数量关系还成立吗?若成立,给出证明,若不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=kx(k≠0)经过点(m,![]() m)(m<0).线段BC的两个端点分别在x轴与直线y=kx上滑动(B、C均与原点O不重合),且BC=
m)(m<0).线段BC的两个端点分别在x轴与直线y=kx上滑动(B、C均与原点O不重合),且BC=![]() .分别作BP⊥x轴,CP⊥直线y=kx,直线BP、CP交于点P.经探究,在整个滑动过程中,O、P两点间的距离为定值,则该距离为_____.
.分别作BP⊥x轴,CP⊥直线y=kx,直线BP、CP交于点P.经探究,在整个滑动过程中,O、P两点间的距离为定值,则该距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BD是对角线.分别过点A、C作AE⊥BD于点E,CF⊥BD于点F,且AE=CF

(1)求证:AB∥CD
(2)若E是BF中点,且△ABE的面积为1,则四边形ABCD的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,DB切⊙O于点B,过点D作DC⊥OA于点C,DC与AB相交于点E.
(1)求证:DB=DE;
(2)若∠BDE=70°,求∠AOB的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为【 】

A.(4![]() +1.6)m B.(12
+1.6)m B.(12![]() +1.6)m C.(4
+1.6)m C.(4![]() +1.6)m D.4
+1.6)m D.4![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某国侦察机![]() 飞抵我国近海搞侦察活动,我战斗机
飞抵我国近海搞侦察活动,我战斗机![]() 奋起拦截,地面雷达测得:当两机都处在雷达的正东方向的上空并在同一高度时,测得它们仰角分别为
奋起拦截,地面雷达测得:当两机都处在雷达的正东方向的上空并在同一高度时,测得它们仰角分别为![]() ,
,![]() ,它们与雷达的距离分别为
,它们与雷达的距离分别为![]() 千米,
千米,![]() 千米,求此时两机距离是多少千米?(精确到
千米,求此时两机距离是多少千米?(精确到![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣4,0),点B的坐标为(0,﹣2),把点A绕点B顺时针旋转90°得到的点C恰好在抛物线y=ax2上,点P是抛物线y=ax2上的一个动点(不与点O重合),把点P向下平移2个单位得到动点Q,则:
(1)直接写出AB所在直线的解析式、点C的坐标、a的值;
(2)连接OP、AQ,当OP+AQ获得最小值时,求这个最小值及此时点P的坐标;
(3)是否存在这样的点P,使得∠QPO=∠OBC,若不存在,请说明理由;若存在,请你直接写出此时P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尊老助老是中华民族的传统美德,我校的小艾同学在今年元旦节前往家附近的敬老院,为老人们表演节目送上新年的祝福,当小艾同学到达敬老院时,发现拷音乐的U盘没有带,于是边打电话给爸爸边往家走,请爸爸能帮忙送来. 3分钟后,爸爸在家找到了U盘并立即前往敬老院,相遇后爸爸将U盘交给小艾,小艾立即把速度提高到之前的1.5倍跑回敬老院,这时爸爸遇到了朋友,停下与朋友交谈了2分钟后,爸爸以原来的速度前往敬老院观看小艾的表演.爸爸与小艾的距离![]() (米)与小艾从敬老院出发的时间
(米)与小艾从敬老院出发的时间![]() (分)之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有______米.
(分)之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有______米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com