
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由根与系数的关系找出“α+β=-2015,α•β=1”,利用整体替换的方法将代数式(α2+2016α+1)(β2+2016β+1)中的1换成αβ,提取公因数代入数据即可得出结论.
解答 解:∵α,β是方程x2+2015x+1=0的两个根,
∴α+β=-2015,αβ=1,
(1+2016α+α2)(1+2016β+β2)
=(αβ+2016α+α2)(αβ+2016β+β2)
=α(β+2016+α)•β(α+2016+β)
=αβ•(2016-2015)(2016-2015)
=1,
故选:A.
点评 本题考查了根与系数的关系,解题的关键是找出“α+β=-2015,α•β=1”.本题属于基础题,难度不大,解决该题型题目时,利用根与系数的关系找出两根之和与两根之积是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
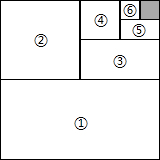 如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com