
 ��ͼ������ԭ���������y=-x2+2mx��m��1����x���������ڵ�A������P��1��m����ֱ��PD��x���ڵ�D�����������ڵ�B���ǵ�B���������߶Գ���ĶԳƵ�ΪC������CB��CP��
��ͼ������ԭ���������y=-x2+2mx��m��1����x���������ڵ�A������P��1��m����ֱ��PD��x���ڵ�D�����������ڵ�B���ǵ�B���������߶Գ���ĶԳƵ�ΪC������CB��CP������ ��1����ȷ��B��1��2m-1���������ߵĶԳ��ᣬ�����öԳ��Եõ�C��2m-1��2m-1�������ǿ���m��ʾBC�ij���
��2���ⷽ��-x2+2mx=0��A��2m��0���������������ľ��빫ʽ�õ�PC2=5m2-10m+5��AC2=4m2-4m+2��PA2=5m2-4m+1��Ȼ�����ù��ɶ����õ�5m2-10m+5+4m2-4m+2=5m2-4m+1���ٽⷽ�̼��ɵõ�m��ֵ��
��3���ٵ�m=$\frac{5}{4}$ʱ�������ߵĽ���ʽΪy=-x2+$\frac{5}{2}$x��C������Ϊ��$\frac{3}{2}$��$\frac{3}{2}$����P������Ϊ��1��$\frac{5}{4}$���������ô���ϵ�������ֱ��PC�Ľ���ʽΪy=$\frac{1}{2}$x+$\frac{3}{4}$����ɵõ�F��$\frac{1}{2}$��1����Ȼ����ݶ��κ���ͼ���ϵ�������������жϵ�F�Ƿ����������ϣ�
����CM��HG��M�����õ��������ε����ʵ�GM=HM����ֱ��PC�Ľ���ʽΪy=$\frac{1}{2}$x+m-$\frac{1}{2}$��ֱ��AC�Ľ���ʽΪy=��-2m+1��x+4m2-2m���ٷֱ����F��3-2m��1����G��$\frac{4{m}^{2}-2m-1}{2m-1}$��1����Ȼ�����������������ʽ�õ���1-3+2m��•��m-1��=2��2m-1-1��•��$\frac{4{m}^{2}-2m-1}{2m-1}$-2m+1����������2m2-7m+5=0�����ǽⷽ�̿ɵõ�m��ֵ��
��� �⣺��1����x=1ʱ��y=-x2+2mx=2m-1����B��1��2m-1����
�����ߵĶԳ���Ϊֱ��x=-$\frac{2m}{2����-1��}$=m��
��C��2m-1��2m-1����
��BC=2m-1-1=2m-2��
��2����y=0ʱ��-x2+2mx=0�����x1=0��x2=2m����A��2m��0����
PC2=��2m-1-1��2+��2m-1-m��2=5m2-10m+5��AC2=��2m-1-2m��2+��2m-1��2=4m2-4m+2��PA2=��2m-1��2+m2=5m2-4m+1��
��PC2+AC2=PA2����PCAΪֱ�������Σ�PC��AC��
��5m2-10m+5+4m2-4m+2=5m2-4m+1��
������2m2-5m+3=0�����m1=$\frac{3}{2}$��m2=1����ȥ����
����mΪ$\frac{3}{2}$ʱ��CA��CP��
��3�����ڣ�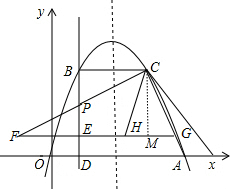
�������£�
��m=$\frac{5}{4}$ʱ�������ߵĽ���ʽΪy=-x2+$\frac{5}{2}$x��C������Ϊ��$\frac{3}{2}$��$\frac{3}{2}$����P������Ϊ��1��$\frac{5}{4}$����
��ֱ��PC�Ľ���ʽΪy=kx+b��
��C��$\frac{3}{2}$��$\frac{3}{2}$����P��1��$\frac{5}{4}$�������$\left\{\begin{array}{l}{\frac{3}{2}k+b=\frac{3}{2}}\\{k+b=\frac{5}{4}}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{3}{4}}\end{array}\right.$��
��ֱ��PC�Ľ���ʽΪy=$\frac{1}{2}$x+$\frac{3}{4}$��
��y=1ʱ��$\frac{1}{2}$x+$\frac{3}{4}$=1�����x=$\frac{1}{2}$����F��$\frac{1}{2}$��1����
��x=$\frac{1}{2}$ʱ��y=-x2+$\frac{5}{2}$x=-$\frac{1}{4}$+$\frac{5}{4}$=1��
���F���������ϣ�
����CM��HG��M����GM=HM��
P��1��m����C��2m-1��2m-1����A��2m��0����
��ֱ��PC�Ľ���ʽΪy=$\frac{1}{2}$x+m-$\frac{1}{2}$��ֱ��AC�Ľ���ʽΪy=��-2m+1��x+4m2-2m��
��y=1ʱ��$\frac{1}{2}$x+m-$\frac{1}{2}$=1�����x=3-2m����F��3-2m��1����
��y=1ʱ����-2m+1��x+4m2-2m=1�����x=$\frac{4{m}^{2}-2m-1}{2m-1}$����G��$\frac{4{m}^{2}-2m-1}{2m-1}$��1����
�ߡ�PFE���CHG�������ȣ�
��$\frac{1}{2}$•EF•PE=2•$\frac{1}{2}$•CM•GM��
����1-3+2m��•��m-1��=2��2m-1-1��•��$\frac{4{m}^{2}-2m-1}{2m-1}$-2m+1��
������2m2-7m+5=0�����m1=$\frac{5}{2}$��m2=1����ȥ����
��m��ֵΪ$\frac{5}{2}$��
�ʴ�Ϊ$\frac{5}{2}$��
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʺ͵��������ε����ʣ������ô���ϵ������һ�κ�������ʽ������������ͼ�����ʣ���ס�����ľ��빫ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 29��33 | B�� | 29��27 | C�� | 30��27 | D�� | 28��27 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��aΪб�ߵ�ֱ�������� | B�� | ��bΪб�ߵ�ֱ�������� | ||
| C�� | ��cΪб�ߵ�ֱ�������� | D�� | ����ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | am+bm-1=m��a+b��-1 | B�� | ��x+2����x-5��=x2-3x-10 | C�� | x2+5x+4=x��x+5+$\frac{4}{x}$�� | D�� | x2-4x=x��x-4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ��ֱ����ֱ�߶Ͽ�����λ����E��D��B��F��ͬһ��ֱ���ϣ�����ADE=140�㣬���DBC�Ķ���Ϊ��������
��ͼ��һ��ֱ����ֱ�߶Ͽ�����λ����E��D��B��F��ͬһ��ֱ���ϣ�����ADE=140�㣬���DBC�Ķ���Ϊ��������| A�� | 30�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
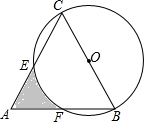 ��ͼ����ABC�ǵȱ������Σ���BCΪֱ����ԲO����AC��AB��E��F���㣬��AB=4������Ӱ���ֵ����Ϊ2$\sqrt{3}$-$\frac{2}{3}$�У�
��ͼ����ABC�ǵȱ������Σ���BCΪֱ����ԲO����AC��AB��E��F���㣬��AB=4������Ӱ���ֵ����Ϊ2$\sqrt{3}$-$\frac{2}{3}$�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
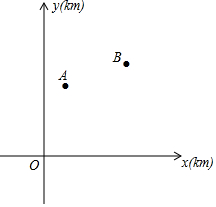 ��A��B������ׯ������ͼֽ�ϵ�����ֱ�Ϊ��2��5������7��7������ͼ��ʾ��x�����ڵ�λ��Ϊһ�����߹�·����Ҫ�ڹ�·����һ��������P��ʹ�÷�����P��������ׯA��B�ľ���֮����С��
��A��B������ׯ������ͼֽ�ϵ�����ֱ�Ϊ��2��5������7��7������ͼ��ʾ��x�����ڵ�λ��Ϊһ�����߹�·����Ҫ�ڹ�·����һ��������P��ʹ�÷�����P��������ׯA��B�ľ���֮����С���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com