
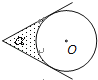
【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A. 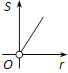 B.
B. 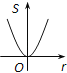 C.
C. 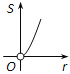 D.
D. 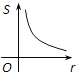
【答案】C
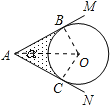
【解析】试题分析:本题主要考查对切线的性质,切线长定理,三角形和扇形的面积,锐角三角函数的定义,四边形的内角和定理等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键. 连接OB、OC、OA,求出∠BOC的度数,求出AB、AC的长,求出四边形OBAC和扇形OBC的面积,即可求出答案.
连接OB、OC、OA,
∵圆O切AM于B,切AN于C,
∴∠OBA=∠OCA=90°,OB=OC=r,AB=AC,
∴∠BOC=360°-90°-90°-α=(180-α)°,
∵AO平分∠MAN,
∴∠BAO=∠CAO=![]() α,
α,
AB=AC=rtan![]() α,
α,
∴阴影部分的面积是:S四边形BACO-S扇形OBC=2×![]() ×
×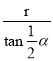 ×r-
×r-![]() =(
=(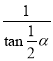 -
-![]() )r2,
)r2,
∵r>0,
∴S与r之间是二次函数关系.
故选C.


科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求本次调查共抽取了多少份书法作品?
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )

A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 哥哥的身高比弟弟高是必然事件
B. 今年的12月1日有雨是不确定事件
C. 随机掷一枚均匀的硬币两次,都是正面朝上是不可能事件
D. “彩票中奖的概率为![]() ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是![]() 的直径,
的直径, ![]() ,连接
,连接![]() .
.

(1)求证: ![]() ;
;
(2)若直线![]() 为
为![]() 的切线,
的切线, ![]() 是切点,在直线
是切点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() 所在的直线与
所在的直线与![]() 所在的直线相交于点
所在的直线相交于点![]() ,连接
,连接![]() .
.
①试探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
②![]() 是否为定值?若是,请求出这个定值;若不是,请说明理由.
是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P是∠ABC内一点.
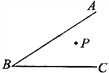
(1)画图:①过点P画BC的垂线,垂足为D;②过点P画BC的平行线交AB于点E,过点P画AB的平行线交BC于点F.
(2)∠EPF等于∠B吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;(2)求证:CD是⊙P的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com