
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,反比例函数y=![]() (k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.
(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.
(1)证明△OCN≌△OAM;
(2)若∠NOM=45°,MN=2,求点C的坐标.

【答案】(1)略(2)(0,![]() ).
).
【解析】
试题分析:(1)由点M、N都在y=![]() 的图象上,即可得出S△ONC=S△OAM=
的图象上,即可得出S△ONC=S△OAM=![]() |k|,再由正方形的性质可得出OC=OA,∠OCN=∠OAM=90°,结合三角形的面积公式即可得出CN=AM,进而即可证出△OCN≌△OAM(SAS);
|k|,再由正方形的性质可得出OC=OA,∠OCN=∠OAM=90°,结合三角形的面积公式即可得出CN=AM,进而即可证出△OCN≌△OAM(SAS);
(2)将△OAM绕点O逆时针旋转90°,点M对应M′,点A对应A′,由旋转和正方形的性质即可得出点A′与点C重合,以及N、C、M′共线,通过角的计算即可得出∠M'ON=∠MON=45°,结合OM′=OM、ON=ON即可证出△M'ON≌△MON(SAS),由此即可得出M′N=MN=2,再由(1)△OCN≌△OAM即可得出CN=AM,通过边与边之间的关系即可得出BM=BN,利用勾股定理即可得出BM=BN=![]() ,设OC=a,则M′N=2CN=2(a﹣
,设OC=a,则M′N=2CN=2(a﹣![]() ),由此即可得出关于a的一元一次方程,解方程即可得出点C的坐标.
),由此即可得出关于a的一元一次方程,解方程即可得出点C的坐标.
试题解析:(1)∵点M、N都在y=![]() 的图象上,
的图象上,
∴S△ONC=S△OAM=![]() |k|.
|k|.
∵四边形ABCO为正方形,
∴OC=OA,∠OCN=∠OAM=90°,
∴![]() OCCN=
OCCN=![]() OAAM.
OAAM.
∴CN=AM.
在△OCN和△OAM中, ,
,
∴△OCN≌△OAM(SAS).
(2)将△OAM绕点O逆时针旋转90°,点M对应M′,点A对应A′,如图所示.
∵OA=OC,
∴OA′与OC重合,点A′与点C重合.
∵∠OCM′+∠OCN=180°,
∴N、C、M′共线.
∵∠COA=90°,∠NOM=45°,
∴∠CON+∠MOA=45°.
∵△OAM旋转得到△OCM′,
∴∠MOA=∠M′OC,
∴∠CON+∠COM'=45°,
∴∠M'ON=∠MON=45°.
在△M'ON与△MON中, ,
,
∴△M'ON≌△MON(SAS),
∴MN=M'N=2.
∵△OCN≌△OAM,
∴CN=AM.
又∵BC=BA,
∴BN=BM.
又∠B=90°,
∴BN2+BM2=MN2,
∴BN=BM=![]() .
.
设OC=a,则CN=AM=a﹣![]() .
.
∵△OAM旋转得到△OCM′,
∴AM=CM'=a﹣![]() ,
,
∴M'N=2![]() ,
,
又∵M'N=2,
∴2(![]() )=2,
)=2,
解得:![]() ,
,
∴C(0,![]() ).
).



 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】据测算,我国每天土地沙漠化造成的经济损失平均为150 000 000元,这个数字用科学记数法表示为( )
A.15×107元B.1.5×108元C.0.15×109元D.1.5×107元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:![]() ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
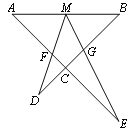
【题目】如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,
且DM交AC于F,ME交BC于G.
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连结FG,如果α=45°,AB=![]() ,AF=3,求FG的长.
,AF=3,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com