练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图一场暴雨后，垂直于地面的一棵树在距地面5米的C处折断，树尖B恰好碰到地面，经测量AB=12米，则原树高为（　　）
    A．22米B．18米C．17米D．13米

    分析 根据题意利用勾股定理得出BC的长，进而得出答案．

    解答 解：由题意得：在直角△ABC中，
    AC2+AB2=BC2，
    则52+122=BC2，
    ∴BC=13米．
    故原树高为：AC+BC=5+13=18（米）．
    故选：B．

    点评 此题主要考查了勾股定理的应用，熟练利用勾股定理得出BC的长是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．计算：$\frac{3}{\sqrt{3}}$+（$\sqrt{3}$-3）0-|-$\sqrt{12}$|-2-1-cos60°=-$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，如果∠1+∠2=180°，∠2+∠3=180°，那么∠1=∠3，理由是同角的补角相等，同理，∠2=∠4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）$\frac{bc}{a^2}$•$\frac{2a}{b^2c}$；                                                     
    （2）$\frac{b}{a^2-9}•\frac{a+3}{b^2-b}$；
    （3）$\frac{x^2+xy}{x-y}÷\frac{xy}{x-y}$；                                                
    （4）$\frac{a}{a-b}•（\frac{b-a}{b}）^2$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知AC，BD与⊙O相切于点A，B，且AC∥BD，若∠COD=90°，求证：CD是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．小刚以0.4千米/分的速度匀速骑车5分钟，在原地休息了6分钟，然后以0.5千米/分的速度骑回出发地，下列函数图象能表达这一过程的是（　　）
    A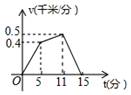．B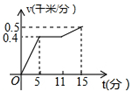．C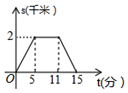．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知多项式x2+2y2-4x+4y+10，其中x，y为任意实数，那么当x，y分别取何值时，多项式的值达到最小值，最小值为（　　）
    A．2B．$\frac{5}{2}$C．4D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．点A在反比例函数y=$\frac{3}{x}$的图象上，过点A作AH⊥x轴于点H，连结OA，tan∠AOH=$\frac{1}{3}$．
    （1）如图，当点A在第一象限时，点A的坐标为（3，1）．
    （2）反比例函数图象上有一动点P，若OA平分∠PAH，则点P的坐标为（$\frac{3}{4}$，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

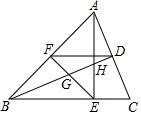    3．如图，在△ABC中，AE和BD是高，∠ABE=45°，点F是AB的中点，BD与FE，AE分别交于点G、H，∠CAE=∠ABD．有下列结论：①FD=FE；②BH=2CD；③BD•BH=2BE2；④S△ABC=$\frac{4}{3}$S四边形BCDF．其中正确的有（　　）
    A．①③B．②④C．①②③D．①②④

    查看答案和解析>>

    同步练习册答案