
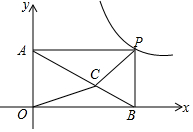
 如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )
如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意作出合适的辅助线,然后根据点P在双曲线y=$\frac{6}{x}$(x>0)上,即可求得△OCB与△ACP的面积和.
解答 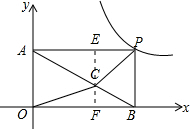 解:作CE⊥AP于点E,作CF⊥OB于点F,
解:作CE⊥AP于点E,作CF⊥OB于点F,
则CE+CF=BP,
设点P的坐标为(p,$\frac{6}{p}$),
∴OB=AP=p,CE+CF=$\frac{6}{p}$,
∴△OCB与△ACP的面积和是:$\frac{OB•CF}{2}+\frac{AP•CE}{2}=\frac{p•\frac{6}{p}}{2}=3$,
故选C.
点评 本题考查反比例函数系数k的几何意义、反比例函数图象上点的坐标特征、平行四边形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用反比例函数的性质解答.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{2}$ | B. | $\frac{1}{3}$x2 | C. | $\frac{x}{π}$ | D. | $\frac{2x+1}{x-3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
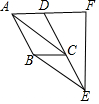 如图,四边形ABCD是平行四边形,E、F分别在DC、AD的延长线上,连接AC、BE,BE∥AC,EF⊥AD,垂足为F,AB=5,DF=4,则EF的长是( )
如图,四边形ABCD是平行四边形,E、F分别在DC、AD的延长线上,连接AC、BE,BE∥AC,EF⊥AD,垂足为F,AB=5,DF=4,则EF的长是( )| A. | $\sqrt{21}$ | B. | 2$\sqrt{21}$ | C. | 10 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com