
 如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是
如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是



 ah=x,根据平行四边形的性质,结合M是AB中点,可得AB=CD=2a,再利用AB∥CD,根据平行线分线段成比例定理的推论可知△BME∽△DCE,根据比例线段易得GH=3h,根据三角形面积公式以及平行四边形的面积公式易求S平行四边形ABCD以及S阴影,进而可求它们的比值.
ah=x,根据平行四边形的性质,结合M是AB中点,可得AB=CD=2a,再利用AB∥CD,根据平行线分线段成比例定理的推论可知△BME∽△DCE,根据比例线段易得GH=3h,根据三角形面积公式以及平行四边形的面积公式易求S平行四边形ABCD以及S阴影,进而可求它们的比值.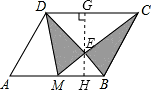 解:如右图,过E作GH⊥CD,分别交AB、CD于H、G,
解:如右图,过E作GH⊥CD,分别交AB、CD于H、G, ah=x,那么
ah=x,那么 AB,
AB, •a•3h-
•a•3h- ah=ah=2x,
ah=ah=2x,

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com