
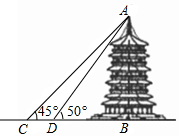
 某中学九年级数学兴趣小组想测量建筑物AB的高度,他们在C处仰望建筑物顶端A,测得仰角为45°,再往建筑物的方向前进3.8米到达D处,测得仰角为50°,AB⊥CB,求建筑物的高度.(测角器的高度忽略不计,结果保留小数点后一位,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
某中学九年级数学兴趣小组想测量建筑物AB的高度,他们在C处仰望建筑物顶端A,测得仰角为45°,再往建筑物的方向前进3.8米到达D处,测得仰角为50°,AB⊥CB,求建筑物的高度.(测角器的高度忽略不计,结果保留小数点后一位,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$x+1=0 | B. | 2x-1=8-x | C. | -3x=1 | D. | x+$\frac{1}{3}$=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com