
 如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB.
如图,在⊙O中,AB为直径,半径OC⊥AB,弦EF经过CO的中点D,EF∥AB. |
| EC |
 |
| EA |
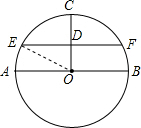 (1)证明:连接OE,
(1)证明:连接OE,| 1 |
| 2 |
 |
| EC |
 |
| EA |
| 1 |
| 2 |
| 1 |
| 2 |
| OE2-OD2 |
| ||
| 2 |
| 3 |


科目:初中数学 来源: 题型:
| 第x(天) | 1≤x≤49 | 50≤x≤90 |
| 当天售价(元/件) | ||
| 当天销量(件) |
查看答案和解析>>
科目:初中数学 来源: 题型:
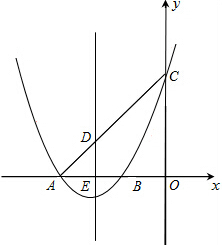 已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式.
已知抛物线y=x2+4x+3交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,求抛物线上是否存在点M,使直线CM把四边形DEOC分成面积相等的两部分?若存在,请写出M所在直线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:
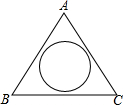 如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.
如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰梯形ABCD中,AD∥BC,将其中一条对角线BD平移到CE的位置,则:
如图,等腰梯形ABCD中,AD∥BC,将其中一条对角线BD平移到CE的位置,则:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com