
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
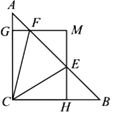
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
【答案】C
【解析】试题解析:①由题意知,△ABC是等腰直角三角形,
∴AB=![]() ,故①正确;
,故①正确;
②如图1,当点E与点B重合时,点H与点B重合,
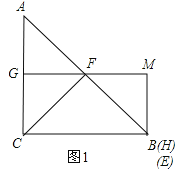
∴MB⊥BC,∠MBC=90°,
∵MG⊥AC,
∴∠MGC=90°=∠C=∠MBC,
∴MG∥BC,四边形MGCB是矩形,
∴MH=MB=CG,
∵∠FCE=45°=∠ABC,∠A=∠ACF=45°,
∴CF=AF=BF,
∴FG是△ACB的中位线,
∴GC=![]() AC=MH,故②正确;
AC=MH,故②正确;
③如图2所示,
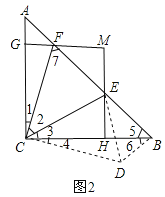
∵AC=BC,∠ACB=90°,
∴∠A=∠5=45°.
将△ACF顺时针旋转90°至△BCD,
则CF=CD,∠1=∠4,∠A=∠6=45°;BD=AF;
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2.
在△ECF和△ECD中,
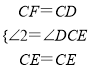 ,
,
∴△ECF≌△ECD(SAS),
∴EF=DE.
∵∠5=45°,
∴∠DBE=90°,
∴DE2=BD2+BE2,即EF2=AF2+BE2,故③错误;
④∵∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE,
∵∠A=∠5=45°,
∴△ACE∽△BFC,
∴![]() ,
,
∴AEBF=ACBC=1,
由题意知四边形CHMG是矩形,
∴MG∥BC,MH=CG,
MG=CH,MH∥AC,
∴![]() ;
; ![]() ,
,
即![]() ;
; ![]() ,
,
∴MG=![]() AE;MH=
AE;MH=![]() BF,
BF,
∴MGMH=![]() AE×
AE×![]() BF=
BF=![]() AEBF=
AEBF=![]()
![]() .
.
故④正确.
故选C.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
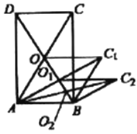
【题目】如图,矩形![]() 的面积为20,对角线
的面积为20,对角线![]() ,
,![]() 交于点
交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ,对角线交于点
,对角线交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.45
D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对校园网站五个栏目的喜爱情况(规定每名学生只能选一个最喜爱的).学校随机抽取了部分学生进行调查,将调查结果整理后绘制成如下两幅不完整的统计图,请结合图中提供的信息解答下列问题:

(1)本次被调查的学生有_____人,扇形统计图中m =_____;
(2) 将条形统计图补充完整;
(3)若该校有1800名学生,估计全校最喜爱“校长信箱”栏目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某长方形广场的四个角都有一个半径相同的四分之一圆形的草地,若圆形的半径为x米,长方形长为a米,宽为b米
(1)分别用代数式表示草地和空地的面积;
(2)若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(计算结果保留到整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数y=|x|-1的性质.
小凡同学根据学习函数的经验,对函数y=|x|-1的图象与性质进行了探究.下面是小凡的探究过程,请补充完整:
(1)在函数y=|x|-1中,自变量x的取值范围是______________;
(2)下表是y与x的几组对应值.
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ||
y | 2 | 1 | 0 | -1 | 0 | 1 | m |
①m=_________;
②若A(n,9),B(10,9)为该函数图象上不同的两点,则_n=__________;
(3)如下图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;

(4)结合函数图象,解决问题:
①函数的最小值为________;
②已知直线![]() 与函数
与函数![]() 的图象交于C,D两点,当y1≥y时x的取值范围是___________.
的图象交于C,D两点,当y1≥y时x的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AE,∠B=∠E,BC=ED,点F是CD的中点,

(1)AC与AD相等吗?为什么?
(2)AF与CD的位置关系如何?说明理由;
(3)若P为AF上的一点,那么PC与PD相等吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com