
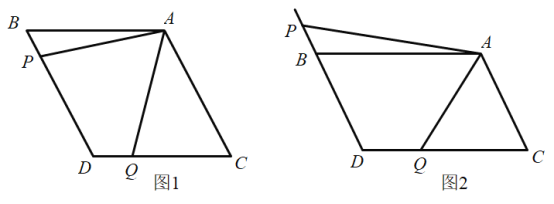
【题目】如图1,![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,且满足
上的点,且满足![]() .
.
(1)求证:![]()
(2)在图1中,是否存在与AP相等的线段?若存在,请找出来,并加以证明;若不存在,说明理由.
(3)若将“![]() 为
为![]() 上的点”改为:“
上的点”改为:“![]() 为DB延长线上的点”其他条件不变(如图2)若
为DB延长线上的点”其他条件不变(如图2)若![]() ,求线段
,求线段![]() 之间的数量关系(用含
之间的数量关系(用含![]() 的式子表示)
的式子表示)
【答案】(1)证明详见解析;(2)存在,![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)由已知可得四边形ABCD是菱形,结合菱形的性质,由![]() 可得
可得![]() ,即可求得
,即可求得![]() ;
;
(2)过点A作![]() ,交BD于点M,证得
,交BD于点M,证得![]() ,得
,得![]() ,即可得AP=AQ;
,即可得AP=AQ;
(3)过点A作![]() ,交BD的延长线于点M,作
,交BD的延长线于点M,作![]() ,可证
,可证![]() ,得
,得![]() ,即
,即![]() ,易证
,易证![]() ,即可得到
,即可得到![]() .
.
(1)证明:∵四边形ABCD是平行四边形,![]() ,
,
∴四边形ABCD是菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)存在,![]() .
.
如图,过点A作![]() ,交BD于点M,
,交BD于点M,
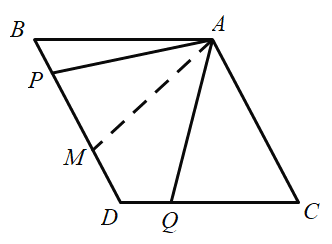
∴∠APM=∠AMP,
由(1)知,![]() ,
,
∴∠APM=∠AQC,
∴∠AMP=∠AQC,
又∵四边形ABCD为菱形,
∴AB=AC,∠B=∠C,
∴![]() ,
,
∴![]() ,
,
即AP=AQ.
(3)过点A作![]() ,交BD的延长线于点M,作
,交BD的延长线于点M,作![]() ,
,

∵四边形ABCD是平行四边形,
∴AC∥BD,∠C+∠BDC=180°,∠ACD=∠ABM,
∵![]() ,
,
∴∠PAQ+∠BDC=180°,
∴∠APB+∠AQD=180°,
∴∠APB=∠AQC,
又∵AP=AM,
∴∠APB=∠AMP,
∴∠AQC=∠AMP,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
在等腰△APM中,AH⊥PM,
∴![]() ,
,
![]() ,
,
即![]() .
.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C,过点C作CD⊥AD于D,AB的延长线与DC的延长线相交于点P,∠ACB的角平分线CE交AB于点F、交⊙O于E.
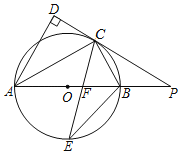
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,直线
与x轴交于点A,与y轴交于点B,直线![]() 与x轴交于点C.
与x轴交于点C.

(1)求点B的坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为G.
围成的区域(不含边界)为G.
①当![]() 时,结合函数图象,求区域G内整点的个数;
时,结合函数图象,求区域G内整点的个数;
②若区域G内恰有2个整点,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(n,![]() 2),B(
2),B(![]() 1,4)是一次函数y=kx+b和反比例函数y=
1,4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
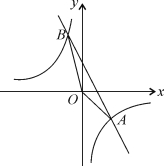
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
(3)直接写出kx+b>![]() 时,
时,![]() 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
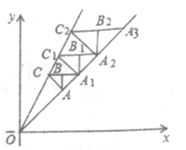
【题目】如图,在平面直角坐标系第一象限内,直线![]() 与直线
与直线![]() 的内部作等腰
的内部作等腰![]() ,使
,使![]() ,边
,边![]() 轴,
轴,![]() 轴,
轴,![]() 在直线
在直线![]() 上,点C在直线
上,点C在直线![]() 上,CB的延长线交直线
上,CB的延长线交直线![]() 于点
于点![]() ,作等腰
,作等腰![]() ,使
,使![]() 轴,
轴,![]() 轴,点
轴,点![]() 在直线
在直线![]() 上,按此规律,则等腰
上,按此规律,则等腰![]() 的腰长为_______.
的腰长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.

求证:
(1)△ABC≌△DCB;
(2)DE·DC=AE·BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[阅读理解]
当![]() 且
且![]() 时,因为
时,因为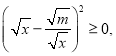 所以
所以![]() 从而
从而![]() (当且仅当
(当且仅当![]() 时取等号).由此可知,在
时取等号).由此可知,在![]() 且
且![]() 的条件下,当
的条件下,当![]() 时,代数式
时,代数式![]() 有最小值为
有最小值为![]() .
.
[实践应用]
(1)在![]() 的条件下,当
的条件下,当![]() 时,
时,![]() 有最小值,且最小值为 ;
有最小值,且最小值为 ;
(2)设![]() ,求
,求![]() 的最小值,并指出当
的最小值,并指出当![]() 取得该最小值时对应的
取得该最小值时对应的![]() 的值;
的值;
[拓展延伸]
在平面直角坐标系中,点![]() 点
点![]() .点
.点![]() 是函数
是函数![]() 在第一象限内图象上的一个动点,过
在第一象限内图象上的一个动点,过![]() 点作
点作![]() 垂直于
垂直于![]() 轴,
轴,![]() 垂直于
垂直于![]() 轴,垂足分别为点
轴,垂足分别为点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.

(3)求![]() 和
和![]() 之间的函数关系式:
之间的函数关系式:
(4)试判断当![]() 的值最小时,四边形
的值最小时,四边形![]() 是何特殊四边形,并说明理由.
是何特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( )
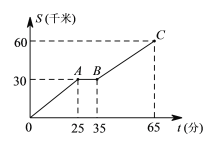
A.汽车行驶到一半路程时,停车加油用时10分钟
B.汽车一共行驶了60千米的路程,上午9点5分到达植物园
C.加油后汽车行驶的速度为60千米/时
D.加油后汽车行驶的速度比加油前汽车行驶的速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
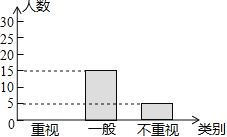
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com