
【题目】如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,有一个只允许单向通过的窄道口,通常情况下,每分钟可以通过9人.一天王老师到达道口时,发现由于拥挤,每分钟只能有3人通过道口,此时,自己前面还有36人等待通过(假定先到达的先过,王老师过道口的时间忽略不计),通过道口后,还需7分钟到达学校.

(1)此时,若绕道而行,要15分钟才能到达学校,从节省时间考虑,王老师应选择绕道去学校,还是选择通过拥挤的道口去学校?
(2)若在王老师等人的维持下,几分钟后秩序恢复正常(维持秩序期间,每分钟仍有3人通过道口),结果王老师比在拥挤的情况下提前6分钟通过道口,问维持秩序的时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
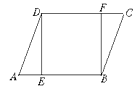
【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
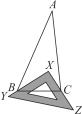
【题目】(1)如图,一个直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C,△ABC中,若∠A=30°,则∠ABC+∠ACB=__ __,∠XBC+∠XCB=__ __;
(2)若改变直角三角板XYZ的位置,但三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请说明理由;若不变化,请求出∠ABX+∠ACX的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ACO以O点为中心,逆时针旋转90°,得Rt△BDO,点B坐标为(0,﹣3),点C坐标为(0, ![]() ),抛物线y=﹣
),抛物线y=﹣ ![]() x2+bx+c经过点A和点C.
x2+bx+c经过点A和点C.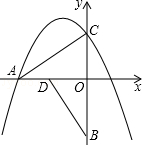
(1)求b,c的值;
(2)在x轴以上的抛物线对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P从点O出发沿x轴向负半轴运动,每秒1个单位,过点P作y轴的平行线交抛物线于点M,当t为几秒时,以M、P、O、C为顶点得四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
查看答案和解析>>
科目:初中数学 来源: 题型:
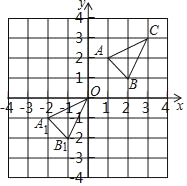
【题目】如图,已知△ABC经过平移后得到△A1B1C1,点A与A1,点B与B1,点C与C1分别是对应点,观察各对应点坐标之间的关系,解答下列问题:
(1)分别写出点A与A1,点B与B1,点C与C1的坐标;
(2)若点P(x,y)通过上述的平移规律平移得到的对应点为Q(3,5),求p点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com