
如图,已知△ABC是面积为 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
解析试题分析:先根据AB=2AD,△ABC∽△ADE,△ABC是面积为 求出△ADE的面积,再判断出△ADE的形状,根据等边三角形的面积求出AE的长,作FG⊥AE于G,由等边三角形及直角三角形的性质判断出△AFG是等腰直角三角形,设AG=FG=h,在直角三角形FGE中利用锐角三角函数的定义即可求出h的值,根据三角形的面积公式即可得出结论.
求出△ADE的面积,再判断出△ADE的形状,根据等边三角形的面积求出AE的长,作FG⊥AE于G,由等边三角形及直角三角形的性质判断出△AFG是等腰直角三角形,设AG=FG=h,在直角三角形FGE中利用锐角三角函数的定义即可求出h的值,根据三角形的面积公式即可得出结论.
解:∵AB=2AD,
∴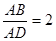
又∵△ABC∽△ADE,△ABC是面积为 ,
,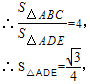
∵△ABC∽△ADE,△ABC是等边三角形,
∴△ADE也是等边三角形,其面积为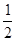 AE•AE•sin60°=
AE•AE•sin60°=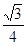 ,即
,即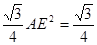 ,解得AE=1,
,解得AE=1,
作FG⊥AE于G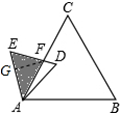
∵∠BAD=45°,∠BAC=∠EAD=60°,
∴∠EAF=45°,
∴△AFG是等腰直角三角形,
设AG=FG=h,在直角三角形FGE中,
∵∠E=60°,EG=1-h,FG=h,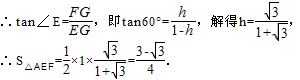
考点:相似三角形的性质,等边三角形的判定,等腰直角三角形的判定
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


科目:初中数学 来源: 题型:填空题
如图,在?ABCD中,E为CD上一点,DE:CE=2:3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有 条.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图是一张锐角三角形纸片,AD是BC边上的高,BC=40cm,AD=30cm,现从硬纸片上剪下一个长是宽2倍的周长最大的矩形,则所剪得的矩形周长为_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知在△ABC中,AB=AC,BC比AB大3, ,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
(1)求AG的长;
(2)当∠APQ=90º时,直线PG与边BC相交于点M.求 的值;
的值;
(3)当点Q在边AC上时,设BP= ,AQ=
,AQ= ,求
,求 关于
关于 的函数解析式,并写出它的定义域.[
的函数解析式,并写出它的定义域.[
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
用纸折出黄金分割点:裁一张正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,这时B″就是AB的黄金分割点,请你证明这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
(2013年四川眉山3分)如图,在函数 (x<0)和
(x<0)和 (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC= ,S△BOC=
,S△BOC= ,则线段AB的长度= .
,则线段AB的长度= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com