
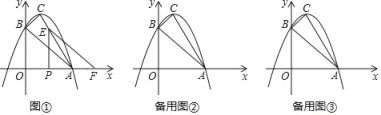
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0).与y轴的交点为B(0,3),其顶点为C.
(1)求抛物线的解析式;
(2)将△AOB沿x轴向右平移m个长度单位(0<m<3)后得到另一个△FPE,点A、O、B的像分别为点F、P、E.
①如图①,当点E在直线AC上时,求m的值.
②设所得的三角形△FPE与△ABC重叠部分的面积为S,求S关于m的函数表达式.
【答案】(1)y=﹣x2+2x+3;(2)①m=![]() ;②当0<m≤
;②当0<m≤![]() 时,S=﹣
时,S=﹣![]() m2+3m;当
m2+3m;当![]() <m<3时,S=
<m<3时,S=![]() m2﹣3m+
m2﹣3m+![]() .
.
【解析】
(1)根据待定系数法可得抛物线的解析式为y=-x2+2x+3.
(2)把点E的坐标代入直线AC的解析式来解答;
(3)平移后的三角形记为△PEF.根据待定系数法可得直线AB的解析式为y=-x+3.易得AB平移m个单位所得直线EF的解析式为y=-x+3+m.连结BE,直线BE交AC于G,则G(![]() ,3).在△AOB沿x轴向右平移的过程中.根据图象,易知重叠部分面积有两种情况:①当0<m≤
,3).在△AOB沿x轴向右平移的过程中.根据图象,易知重叠部分面积有两种情况:①当0<m≤![]() 时;②当
时;②当![]() <m<3时;讨论可得用m的代数式表示S.
<m<3时;讨论可得用m的代数式表示S.
(1)由题意可知,抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),则![]() ,解得
,解得![]() .
.
故抛物线的解析式为y=﹣x2+2x+3.
(2)由题意知,E(m,3).
由(1)得:y=﹣x2+2x+3=﹣(x﹣1)2+4,故C(1,4).
设直线AC的解析式为y=kx+t(k≠0).
把A(3,0),C(1,4)代入,得![]() .
.
解得![]() .
.
故直线AC的解析式为:y=﹣2x+6.
把E(m,3)代入知,﹣2m+6=3
解得m=![]() ;
;
(3)平移后的三角形记为△PEF.
设直线AB的解析式为y=k′x+d,则![]() ,
,
解得![]() .
.
则直线AB的解析式为y=﹣x+3.
△AOB沿x轴向右平移m个单位长度(0<m<3)得到△PEF,
易得直线EF的解析式为y=﹣x+3+m.
由(2)知,直线AC的解析式为y=﹣2x+6.
连结BE,直线BE交AC于G,则G(![]() ,3).
,3).
在△AOB沿x轴向右平移的过程中.
①当0<m≤![]() 时,如图1所示.
时,如图1所示.
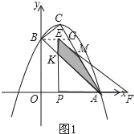
设PE交AB于K,EF交AC于M.
则BE=EK=m,PK=PA=3﹣m,
联立![]() ,解得
,解得![]() ,
,
即点M(3﹣m,2m).
故S=S△PEF﹣S△PAK﹣S△AFM
=![]() PE2﹣
PE2﹣![]() PK2﹣
PK2﹣![]() Fh
Fh
=![]() ﹣
﹣![]() (3﹣m)2﹣
(3﹣m)2﹣![]() m2m
m2m
=﹣![]() m2+3m.
m2+3m.
②当![]() <m<3时,如图2所示.
<m<3时,如图2所示.
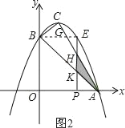
设PE交AB于K,交AC于H.
因为BE=m,所以PK=PA=3﹣m,
又因为直线AC的解析式为y=﹣2x+6,
所以当x=m时,得y=6﹣2m,
所以点H(m,6﹣2m).
故S=S△PAH﹣S△PAK
=![]() PAPH﹣
PAPH﹣![]() PA2
PA2
=﹣![]() (3﹣m)(6﹣2m)﹣
(3﹣m)(6﹣2m)﹣![]() (3﹣m)2
(3﹣m)2
=![]() m2﹣3m+
m2﹣3m+![]() .
.
综上所述,当0<m≤![]() 时,S=﹣
时,S=﹣![]() m2+3m;当
m2+3m;当![]() <m<3时,S=
<m<3时,S=![]() m2﹣3m+
m2﹣3m+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在﹣9,﹣6,﹣3,﹣1,2,3,6,8,11这九个数中,任取一个作为a值,能够使关于x的一元二次方程x2+ax+9=0有两个不相等的实数根的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
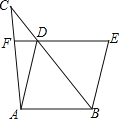
【题目】如图,在△ABC中,点D在BC边上,BC=3CD,分别过点B,D作AD,AB的平行线,并交于点E,且ED交AC于点F,AD=3DF.
(1)求证:△CFD∽△CAB;
(2)求证:四边形ABED为菱形;
(3)若DF=![]() ,BC=9,求四边形ABED的面积.
,BC=9,求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O作EF∥BC,EF与AB、CD分别相交于点E、F,则△DOF的面积与△BOA的面积之比为( )
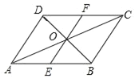
A. 1:2B. 1:4C. 1:8D. 1:16
查看答案和解析>>
科目:初中数学 来源: 题型:
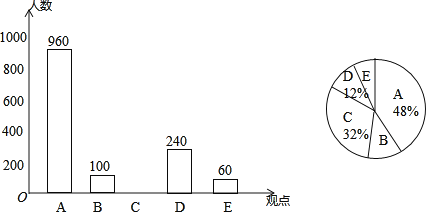
【题目】某公益机构为了解市民使用“手机阅读”的情况,对部分市民进行了随机问卷调查(问卷调查表如左图所示),并将调查结果绘制成两副统计图(均不完整)
您如何看待手机阅读问卷调查表 您好!请在表格中选择一项您最认同的观点,在其后面空格内打“√”,非常感谢您的配合. | ||
选项 | 观点 | 您的选择 |
A | 更新及时 | □ |
B | 阅读成本低 | □ |
C | 不利于人际交往 | □ |
D | 内容丰富 | □ |
E | 其他 | □ |
(1)本次接受调查的总人数是______人.
(2)请将条形统计图补充完整.
(3)在扇形统计图中,表示观点B的扇形的圆心角度数为______度.
(4)根据上述调查结果,请估计在2万名市民中,认为手机阅读“内容丰富“的大约有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,则下面说法正确的是( )
A. 1一定不是方程x2+bx+a=0的根B. 0一定不是方程x2+bx+a=0的根
C. ﹣1可能是方程x2+bx+a=0的根D. 1和﹣1都是方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
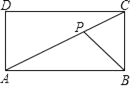
【题目】如图,点P是矩形ABCD的对角线AC上的一点(异于两个端点),AB=2BC=2,若BP的垂直平分线EF经过该矩形的一个顶点,则BP的垂直平分线EF与对角线AC的夹角(锐角)的正切值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com