
”¾ĢāÄæ”æ”°ŹéĻć³¤É³2019ŹĄ½ē¶ĮŹéČÕ”±ĻµĮŠÖ÷Ģā»ī¶Æ¼¤·¢ĮĖѧɜµÄŌĶĮŠĖȤ£¬ĪŅŠ£ĪŖĀś×ćѧɜµÄŌĶĮŠčĒó£¬Óū¹ŗ½ųŅ»ÅśŃ§ÉśĻ²»¶µÄĶ¼Źé£¬Ń§Š£×éÖÆѧɜ»į³ÉŌ±Ė껜³éČ”²æ·Öѧɜ½ųŠŠĪŹ¾ķµ÷²é£¬±»µ÷²éѧɜŠė“Ó”°ĪÄŹ·Ąą”¢¶ÅæĘĄą”¢Š”ĖµĄą”¢Éś»īĄą”±ÖŠŃ”Ōń×Ō¼ŗĻ²»¶µÄŅ»Ąą£¬øł¾Żµ÷²é½į¹ū»ęÖĘĮĖĶ³¼ĘĶ¼£ØĪ“Ķź³É£©£¬Ēėøł¾ŻĶ¼ÖŠŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
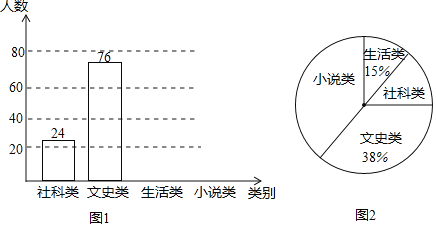
£Ø1£©“Ė“Ī¹²µ÷²éĮĖ”” ””Ćūѧɜ£»
£Ø2£©½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©Ķ¼2ÖŠ”°Š”ĖµĄą”±ĖłŌŚÉČŠĪµÄŌ²ŠÄ½ĒĪŖ”” ””¶Č£»
£Ø4£©ČōøĆŠ£¹²ÓŠŃ§Éś3000ČĖ£¬¹Ą¼ĘøĆŠ£Ļ²»¶”°ĪÄŹ·Ąą”±Źé¼®µÄѧɜČĖŹż£®
”¾“š°ø”æ£Ø1£©200£»£Ø2£©Ļź¼ū½āĪö£»£Ø3£©126”ć£»£Ø4£©1140ČĖ£®
”¾½āĪö”æ
£Ø1£©øł¾ŻŃ”ŌńĪÄŹ·ĄąµÄČĖŹżÓė°Ł·Ö±Č¼“æÉµĆ½ā£»
£Ø2£©ÓÉ£Ø1£©ÓėŃ”ŌńÉś»īĄąµÄ°Ł·Ö±ČĻČĒó³öŃ”ŌńÉś»īĄąµÄČĖŹż£¬ŌŁĒó³öŃ”ŌńŠ”ĖµĄąµÄČĖŹż¼“æÉ£»
£Ø3£©ÓĆ360”ć”ĮŃ”ŌńŠ”ĖµĄąµÄ°Ł·Ö±Č¼“æÉµĆ½ā£»
£Ø4£©ÓĆ×ÜČĖŹż”ĮĻ²»¶ĪÄŹ·ĄąµÄ°Ł·Ö±Č¼“æÉ.
½ā£ŗ£Ø1£©76”Ā38%£½200ČĖ£¬
¹Ź“š°øĪŖ£ŗ200£®
£Ø2£©200”Į15%£½30ČĖ£¬200©24©76©30£½70ČĖ£¬²¹Č«ĢõŠĪĶ³¼ĘĶ¼ČēĶ¼ĖłŹ¾£ŗ

£Ø3£©360”ć”Į![]() £½126”ć£¬
£½126”ć£¬
¹Ź“š°øĪŖ£ŗ126”ć£®
£Ø4£©3000”Į38%£½1140ČĖ£¬
“š£ŗøĆŠ£3000ČĖѧɜ֊Ļ²»¶”°ĪÄŹ·Ąą”±Źé¼®µÄѧɜČĖŹż1140ČĖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģ£ŗx2©£Øm©3£©x©m=0
£Ø1£©Ö¤Ć÷Ō·½³ĢÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£»
£Ø2£©ČōÅ×ĪļĻßy=x2©£Øm©3£©x©mÓėxÖį½»ÓŚA£Øx1£¬0£©£¬B£Øx2£¬0£©Į½µć£¬ŌņA£¬BĮ½µć¼äµÄ¾ąĄėŹĒ·ń“ęŌŚ×ī“ó»ņ×īŠ”Öµ£æČō“ęŌŚ£¬Ēó³öÕāøöÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®£ØÓŃĒéĢįŹ¾£ŗAB=|x1©x2|£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×Ō2020ÄźæŖŹ¼£¬ŠĀ¹Ś²”¶¾ŅßĒéŃĻ¾ž£¬Ä³°®ŠÄ×éÖƽō¼±³ļ¼ÆĮĖ²æ·Ö׏½š£¬¼Ę»®¹ŗĀņ¼×”¢ŅŅĮ½ÖÖ¾ČŌÖĪļĘ·¹²4000¼žĖĶĶłĪäŗŗ£¬ŅŃÖŖĆ漞¼×ÖÖĪļĘ·µÄ¼Ūøń±ČĆ漞ŅŅÖÖĪļĘ·µÄ¼Ūøń¹ó10ŌŖ£¬ÓĆ450ŌŖ¹ŗĀņ¼×ÖÖĪļĘ·µÄ¼žŹżĒ”ŗĆÓėÓĆ400ŌŖ¹ŗĀņŅŅÖÖĪļĘ·µÄ¼žŹżĻąĶ¬£®
£Ø1£©Ēó¼×”¢ŅŅĮ½ÖÖ¾ČŌÖĪļĘ·Ć漞µÄ¼Ūøń·Ö±šŹĒ¶ąÉŁŌŖ£æ
£Ø2£©¾µ÷²é£¬ŌÖĒų¶ŌŅŅÖÖĪļĘ·¼žŹżŠčĒóĮæŹĒ¼×ÖÖĪļĘ·¼žŹżµÄ3±¶£¬ČōøĆ°®ŠÄ×éÖÆ°“ÕÕ“ĖŠčĒóµÄ±ČĄż¹ŗĀņÕā4000¼žĪļĘ·£¬Šč³ļ¼Æ׏½š¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠÓŠRt”÷ABC£¬”ĻA£½90”ć£¬AB£½AC£¬A£Ø£2£¬0£©”¢B£Ø0£¬ d£©”¢C£Ø£3£¬2£©.
£Ø1£©ĒódµÄÖµ£»
£Ø2£©½«”÷ABCŃŲ![]() ÖįµÄÕż·½ĻņĘ½ŅĘaøöµ„Ī»£¬ŌŚµŚŅ»ĻóĻŽÄŚB”¢CĮ½µćµÄ¶ŌÓ¦µćB”䔢C”äÕżŗĆĀäŌŚÄ³·“±ČĄżŗÆŹżĶ¼ĻńÉĻ.ĒėĒó³öÕāøö·“±ČĄżŗÆŹżŗĶ“ĖŹ±Ö±ĻßB”äC”äµÄ½āĪöŹ½£»
ÖįµÄÕż·½ĻņĘ½ŅĘaøöµ„Ī»£¬ŌŚµŚŅ»ĻóĻŽÄŚB”¢CĮ½µćµÄ¶ŌÓ¦µćB”䔢C”äÕżŗĆĀäŌŚÄ³·“±ČĄżŗÆŹżĶ¼ĻńÉĻ.ĒėĒó³öÕāøö·“±ČĄżŗÆŹżŗĶ“ĖŹ±Ö±ĻßB”äC”äµÄ½āĪöŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Ö±Ļß![]() ½»yÖįÓŚµćG£¬×÷
½»yÖįÓŚµćG£¬×÷![]() ”Ķ
”Ķ![]() ÖįÓŚ
ÖįÓŚ![]() £®
£® ![]() ŹĒĻ߶Ī
ŹĒĻ߶Ī![]() ÉĻµÄŅ»µć£¬Čō”÷
ÉĻµÄŅ»µć£¬Čō”÷![]() ŗĶ”÷
ŗĶ”÷![]() Ć껿ĻąµČ£¬Ēóµć
Ć껿ĻąµČ£¬Ēóµć![]() ×ų±ź£®
×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ĆæŅ»øöŠ”·½øńµÄ±ßøö³¤ĪŖ1øöµ„Ī»£®

£Ø1£©ĒėŠ“³ö”÷ABCø÷µćµÄ×ų±ź£»
£Ø2£©Čō°Ń”÷ABCĻņÉĻĘ½ŅĘ2øöµ„Ī»£¬ŌŁĻņÓŅĘ½ŅĘ2øöµ„Ī»µĆµ½”÷A1B1C1£¬ŌŚĶ¼ÖŠ»³ö”÷A1B1C1£»
£Ø3£©Ēó”÷A1B1C1µÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
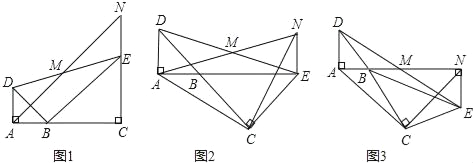
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷BADŗĶ”÷BCE¾łĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻBAD=”ĻBCE=90”ć£¬µćMĪŖDEµÄÖŠµć£¬¹żµćEÓėADĘ½ŠŠµÄÖ±Ļß½»ÉäĻßAMÓŚµćN£®
£Ø1£©µ±A£¬B£¬CČżµćŌŚĶ¬Ņ»Ö±ĻßÉĻŹ±£ØČēĶ¼1£©£¬Ö±½ÓŠ“³öĻ߶ĪADÓėNEµÄŹżĮæ¹ŲĻµĪŖ”” ””£®
£Ø2£©½«Ķ¼1ÖŠµÄ”÷BCEČʵćBŠż×Ŗ£¬µ±A£¬B£¬EČżµćŌŚĶ¬Ņ»Ö±ĻßÉĻŹ±£ØČēĶ¼2£©£¬ÅŠ¶Ļ”÷ACNŹĒŹ²Ć“ĢŲŹāČż½ĒŠĪ²¢ĖµĆ÷ĄķÓÉ£®
£Ø3£©½«Ķ¼1ÖŠ”÷BCEČʵćBŠż×Ŗµ½Ķ¼3Ī»ÖĆ£¬“ĖŹ±A£¬B£¬MČżµćŌŚĶ¬Ņ»Ö±ĻßÉĻ£®ČōAC=3![]() £¬AD=1£¬ŌņĖıߊĪACENµÄĆ껿ĪŖ”” ””£®
£¬AD=1£¬ŌņĖıߊĪACENµÄĆ껿ĪŖ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
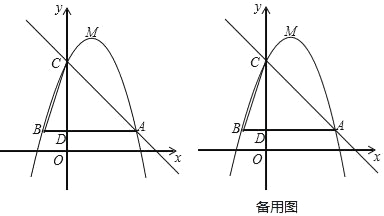
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹży=©x2+bx+c£ØĘäÖŠb£¬cĪŖ³£Źż£©µÄĶ¼Ļó¾¹żµćA£Ø3£¬1£©£¬µćC£Ø0£¬4£©£¬¶„µćĪŖµćM£¬¹żµćA×÷AB”ĪxÖį£¬½»yÖįÓŚµćD£¬½»øƶž“ĪŗÆŹżĶ¼ĻóÓŚµćB£¬Į¬½įBC£®
£Ø1£©Ēóøƶž“ĪŗÆŹżµÄ½āĪöŹ½¼°µćMµÄ×ų±ź£®
£Ø2£©Čō½«øƶž“ĪŗÆŹżĶ¼ĻóĻņĻĀĘ½ŅĘm£Øm£¾0£©øöµ„Ī»£¬Ź¹Ę½ŅĘŗóµĆµ½µÄ¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶„µćĀäŌŚ”÷ABCµÄÄŚ²æ£Ø²»°üĄØ”÷ABCµÄ±ß½ē£©£¬ĒómµÄȔֵ·¶Ī§£®
£Ø3£©ŃŲÖ±ĻßAC·½ĻņĘ½ŅĘøƶž“ĪŗÆŹżĶ¼Ļó£¬Ź¹µĆCMÓėĘ½ŅĘĒ°µÄCBĻąµČ£¬ĒóĘ½ŅĘŗóµćMµÄ×ų±ź£®
£Ø4£©µćPŹĒÖ±ĻßACÉĻµÄ¶Æµć£¬¹żµćP×÷Ö±ĻßACµÄ“¹ĻßPQ£¬¼ĒµćM¹ŲÓŚÖ±ĻßPQµÄ¶Ō³ĘµćĪŖM”䣮µ±ŅŌµćP”¢A”¢M”¢M”äĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪŹ±£¬Ö±½ÓŠ“³öµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»øöÕż·½ŠĪÄŚĮ½øöĻąĮŚÕż·½ŠĪµÄĆ껿·Ö±šĪŖ 4 ŗĶ 2£¬ĖüĆĒ¶¼ÓŠĮ½øö¶„µćŌŚ“óÕż·½ŠĪµÄ±ß ÉĻĒŅ×é³ÉµÄĶ¼ŠĪĪŖÖį¶Ō³ĘĶ¼ŠĪ£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ______£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
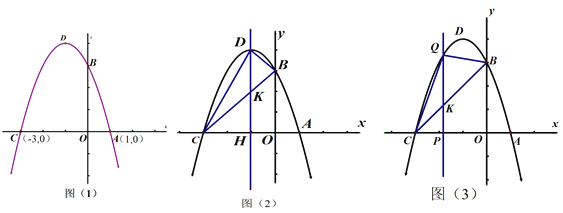
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼£¬Å×ĪļĻßÓėxÖį½»µć×ų±źĪŖA£Ø1£¬0£©£¬C£Ø-3£¬0£©£¬
£Ø1£©ČōŅŃÖŖ¶„µć×ų±źDĪŖ£Ø-1£¬4£©»ņBµć£Ø0£¬3£©£¬Ń”ŌńŹŹµ±·½Ź½ĒóÅ×ĪļĻߵĽāĪöŹ½.
£Ø2£©ČōÖ±ĻßDHĪŖÅ×ĪļĻߵĶŌ³ĘÖį£¬ŌŚ£Ø1£©µÄ»ł“”ÉĻ£¬ĒóĻ߶ĪDKµÄ³¤¶Č£¬²¢Ēó”÷DBCµÄĆ껿£®
£Ø3£©½«Ķ¼£Ø2£©ÖŠµÄ¶Ō³ĘÖįĻņ×óŅĘ¶Æ£¬½»xÖįÓŚµćp£Øm£¬0£©(£3<m<£1)£¬ÓėĻ߶ĪBC”¢Å×ĪļĻߵĽ»µć·Ö±šĪŖµćK”¢Q£¬ÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾QKµÄ³¤¶Č£¬²¢Ēó³öµ±mĪŖŗĪÖµŹ±£¬”÷BCQµÄĆ껿×ī“ó£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com