
����Ŀ����֪������y��ax2+bx+2����A����1��0����B��2��0����C���㣮ֱ��y��mx+![]() ����������A��Q���㣬��P����������ֱ��AQ�Ϸ���һ�����㣬��PF��x�ᣬ����ΪF����AQ�ڵ�N��
����������A��Q���㣬��P����������ֱ��AQ�Ϸ���һ�����㣬��PF��x�ᣬ����ΪF����AQ�ڵ�N��

��1���������ߵĽ���ʽ��
��2����ͼ��������P�˶���ʲôλ��ʱ���߶�PN��2NF�������ʱ��P�����ꣻ
��3����ͼ�����߶�AC�Ĵ�ֱƽ���߽�x���ڵ�E������ΪD����MΪ�����ߵĶ��㣬��ֱ��DE���Ƿ����һ��G��ʹ��CMG���ܳ���С�������ڣ��������G�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+x+2����2����P������Ϊ��![]() ��
��![]() ������3����ֱ��DE�ϴ���һ��G��ʹ��CMG���ܳ���С����ʱG����
������3����ֱ��DE�ϴ���һ��G��ʹ��CMG���ܳ���С����ʱG����![]() ��
��![]() ����
����
��������
��1������A�͵�B��������������ߵĽ���ʽ�õ�����b��c�ķ����飬Ȼ�����a��b��ֵ���Ӷ��õ�����Ĵ𰸣�
��2����A����1��0������y��mx+![]() ���m��ֵ���ɵõ�ֱ��AQ�Ľ���ʽ�����P�ĺ�����Ϊn����P��n����n2+n+2����N��n��
���m��ֵ���ɵõ�ֱ��AQ�Ľ���ʽ�����P�ĺ�����Ϊn����P��n����n2+n+2����N��n��![]() n+
n+![]() ����F��n��0����
����F��n��0����
Ȼ���ú�n��ʽ�ӱ�ʾ��PN��NF�ij���Ȼ������PN��2NF�з�����⼴�ɣ�
��3������AM��ֱ��DE���G������CG��CM��ʱ����CMG���ܳ���С������õ�M�����꣬Ȼ�����AM��DE�Ľ���ʽ������������ֱ�ߵĽ������꼴�ɣ�
��1����������y��ax2+bx+2����A����1��0����B��2��0����
�ཫ��A�͵�B���������ã�![]() �����a����1��b��1��
�����a����1��b��1��
�������ߵĽ���ʽΪy����x2+x+2��
��2��ֱ��y��mx+![]() ����������A��Q���㣬��A����1��0���������ʽ�ã�m��
����������A��Q���㣬��A����1��0���������ʽ�ã�m��![]() ��
��
��ֱ��AQ�Ľ���ʽΪy��![]() x+
x+![]() ��
��
���P�ĺ�����Ϊn����P��n����n2+n+2����N��n��![]() n+
n+![]() ����F��n��0����
����F��n��0����
��PN����n2+n+2����![]() n+
n+![]() ������n2+
������n2+![]() n+
n+![]() ��NF��
��NF��![]() n+
n+![]() ��
��
��PN��2NF������n2+![]() n+
n+![]() ��2����
��2����![]() n+
n+![]() ������ã�n����1��
������ã�n����1��![]() ��
��
��n����1ʱ����P���A�غϣ�������������ȥ��
���P��������![]() ��
��![]() ����
����
��3����y����x2+x+2��������x��![]() ��2+
��2+![]() ��
��
��M��![]() ��
��![]() ����
����
��ͼ��ʾ������AM��ֱ��DE���G������CG��CM��ʱ����CMG���ܳ���С��

��ֱ��AM�ĺ�������ʽΪy��kx+b���ҹ�A����1��0����M��![]() ��
��![]() ����
����
��������ã� �����
�����![]() ��
��
��ֱ��AM�ĺ�������ʽΪy��![]() x+
x+![]() ��
��
��DΪAC���е㣬
��D����![]() ��1����
��1����
��ֱ��AC�Ľ���ʽΪy��kx+2������A���������ã���k+2��0�����k��2��
��AC�Ľ���ʽΪy��2x+2��
��ֱ��DE�Ľ���ʽΪy����![]() x+c������D���������ã�
x+c������D���������ã�![]() +c��1�����c��
+c��1�����c��![]() ��
��
��ֱ��DE�Ľ���ʽΪy����![]() x+
x+![]() ��
��
��y����![]() x+
x+![]() ��y��
��y��![]() x+
x+![]() ��������ã�x����
��������ã�x����![]() ��y��
��y��![]() ��
��
����ֱ��DE�ϴ���һ��G��ʹ��CMG���ܳ���С����ʱG����![]() ��
��![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�Rt��OCD��һ��OC��x���ϣ���OCD��90�㣬��D�ڵ�һ���ޣ�OC��6��DC��4��������������ͼ��OD���е�A��
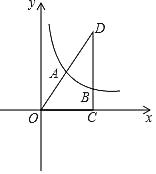
��1����÷����������Ľ���ʽ��
��2�����÷�����������ͼ����Rt��OCD����һ��DC���ڵ�B�����A��B�����ֱ�ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ƽ������˶��ķ�չ��ijУ��֯У�������˶��ᣬ����������������ë��ƹ�������Ҫ��ÿλѧ������μ�һ���ֻ�ܲμ�һ�ij����һ��ѧ�������Լ��˽�İ��������������ͼ��ʾ�IJ�����ͳ�Ʊ�������ͳ��ͼ.

�����ͼ�����ṩ����Ϣ������������⣺
��1��ͼ����m=________��n=________��
��2������Уѧ������1000�ˣ����У�μ���ë��������ԼΪ________�ˣ�
��3���ð�μ�ƹ������4λͬѧ�У���3λ��ͬѧ���ֱ���A��B��C��ʾ����1λŮͬѧ����D��ʾ������������ѡ������ͬѧ�μ�˫�����������״ͼ���б������ǡ��ѡ��һ��һŮ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪��![]() ������Ϊ
������Ϊ![]() .
.
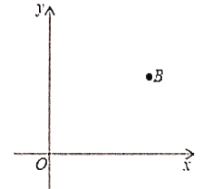
��1������ֱ�ߣ������̶ȣ���Բ����һ��ֱ��![]() ������
������![]() ���
���![]() ���������ֱ��ڵ�
���������ֱ��ڵ�![]() �͵�
�͵�![]() ����
����![]() ��
��![]() ����ֱ��
����ֱ��![]() �Գ�.����ͼ����д��������Ҫ������ͼ�ۼ�.��
�Գ�.����ͼ����д��������Ҫ������ͼ�ۼ�.��
��2���������1����������ֱ��![]() �ĺ�������ʽ.
�ĺ�������ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�������ⷢ�֡�
��ͼ1����Rt��ABC�У�AB=AC=2����BAC=90�㣬��DΪBC���е㣬��CDΪһ����������CDEF����Eǡ�����A�غϣ����߶�BE��AF��������ϵΪ�� ��
��2������չ�о���
�ڣ�1���������£����������CDEF�Ƶ�C��ת������BE��CE��AF���߶�BE��AF��������ϵ���ޱ仯�������ͼ2�����θ���֤����
��3�������ⷢ�֡�
��������CDEF��ת��B��E��F���㹲��ʱ��ֱ��д���߶�AF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ�˽����ν̵��������ѧ����ѧѧϰ���������ѧ������һ�β��ԣ������������ijɼ����ٷ��ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
��A��B����ѧ�����������������ͬ����ѧ�ɼ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�5�飺x<60��60��x<70��70��x<80��80��x<90��90��x��100����
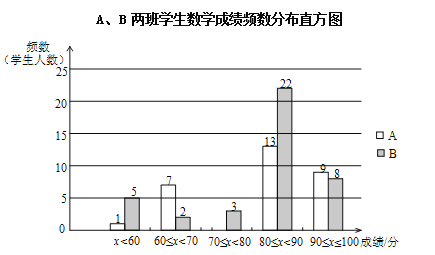
��A��B����ѧ�����Գɼ���80��x<90��һ����������£�
A�ࣺ80 80 82 83 85 85 86 87 87 87 88 89 89
B�ࣺ80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
��A��B����ѧ�����Գɼ���ƽ��������λ�����������£�
ƽ���� | ��λ�� | ���� | |
A�� | 80.6 | m | 96.9 |
B�� | 80.8 | n | 153.3 |
����������Ϣ���ش��������⣺
��1����ȫ��ѧ�ɼ�Ƶ���ֲ�ֱ��ͼ��
��2��д������m��n��ֵ��
��3������Աȷ���A��B����ѧ������ѧѧϰ��������ٴ�������ͬ�ĽǶȷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�е���������M![]() ��N
��N![]() ���������¶��壺��M���N�ġ����߾��롱Ϊ��
���������¶��壺��M���N�ġ����߾��롱Ϊ��![]()
![]()
![]() ��
��

���磺����M(-1��1)����N(2��-2)�����M���N�ġ����߾��롱Ϊ��![]() ���������϶��壬����������⣺
���������϶��壬����������⣺
��1����֪��P(3��-2)��
������A(-2��-1)����d(P��A)= ��
������B(b��2)����d(P��B)=5����b= ��
����֪��C��m,n����ֱ��![]() �ϵ�һ�����㣬��d(P��C)<3����m��ȡֵ��Χ��
�ϵ�һ�����㣬��d(P��C)<3����m��ȡֵ��Χ��
��2����F�İ뾶Ϊ1��Բ��F������Ϊ(0��t)������F�ϴ��ڵ�E��ʹd(E��O)=2��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ, �ڶ�������ĺ�����MN����A��B���ۿڣ�������һ��С��P������ÿ�춼���ִ���A��B ���ۿ���AP��BP��·��ȥС��������ҵ����֪С��P��A�۵ı�ƫ��60��������B�۵ı�ƫ��45������С��P�ຣ����MN�ľ���Ϊ30����.
(1)��AP��BP�ij�(�ο����ݣ�![]() ��1.4��
��1.4��![]() ��1.7��
��1.7��![]() ��2.2)��
��2.2)��
(2)�ס��������ֱ��A��B���ۿ�ͬʱ����ȥС��P������ҵ���״����Ҵ�����С��24���ӣ���֪�״��ٶ����Ҵ��ٶȵ�1.2��������(1)�еĽ����ס����������ٶȸ��Ƕ��ٺ���/ʱ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����x+4�ֱ�x�ᡢy����A��C���㣬������y����x2+mx+4������A������x�����һ������Ϊ��B������BC������C��CD��x�ύ�������ڵ�D

��1���������ߵĺ�������ʽ��
��2������E���������ϵĵ㣬�������ECD����BCO�ĵ�E�����ꣻ
��3����M��y������λ�ڵ�C�Ϸ�����N��ֱ��AC�ϣ���PΪ��һ�����ڵ���������һ�㣬���Ե�C��M��N��PΪ������ı��������Σ������εı߳���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com