练习册

  • 练习册
  • 试题
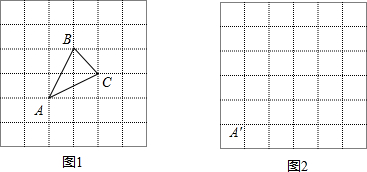
    精英家教网 > 初中数学 > 题目详情
    如图所示，由点B观察点A的方向是（　　）
    分析：根据平行线的性质求出∠ABE，求出∠CBA，根据图形和角的度数即可得出答案．
    解答：解：
    ∵东西方向是平行的，
    ∴∠ABE=∠DAB=62°，
    ∵∠CBE=90°，
    ∴∠CBA=90°-62°=28°，
    即由点B观察点A的方向是北偏东28°，
    故选B．
    点评：本题考查了平行线的性质和方向角的应用，主要考查学生的计算能力和观察图形的能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    21、△ABC在方格纸中位置如图所示
    （1）请在方格纸上建立平面直角坐标系，使得A、B两点的坐标分别为A（2，-1）、B（1，-4），并求出C点的坐标；
    （2）作出△ABC关于横轴对称的△A1B1C1，再作出△ABC以坐标原点为旋转中心、旋转180°后的△A2B2C2，并写C1，C2两点的坐标；
    （3）观察△A1B1C1和△A2B2C2，其中的一个三角形能否由另一个三角形经过某种变换而得到？若能，请指出什么变换．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下列材料：
    正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．
    数学老师给小明同学出了一道题目：在图1正方形网格（每个小正方形边长为1）中画出格点△ABC，使AB=AC=
    		5
    ，BC=
    		2
    ；
    小明同学的做法是：由勾股定理，得AB=AC=
    		22+12
    =
    		5
    ，BC=
    		12+12
    =
    		2
    ，于是画出线段AB、AC、BC，从而画出格点△ABC．
    （1）请你参考小明同学的做法，在图2正方形网格（每个小正方形边长为1）中画出格点△A′B′C′（A′点位置如图所示），使A′B′=A′C′=5，B′C′=
    		10
    ．（直接画出图形，不写过程）；
    （2）观察△ABC与△A′B′C′的形状，猜想∠BAC与∠B′A′C′有怎样的数量关系，并证明你的猜想．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•建阳市模拟）小刘同学在课外活动中观察吊车的工作过程，绘制了如图所示的平面图形．已知吊车吊臂的支点O距离地面的高度OO′=2米．当吊臂顶端由A点抬升至A′点（吊臂长度不变）时，地面B处的重物（大小忽略不计）被吊到B′处，紧绷着的吊绳A′B′=AB．AB垂直地面O′B于点B，A′B′垂直地面O′B于点C，吊臂长度OA′=OA=10米，且cosA=
    3
    5
    ，sinA′=
    1
    2
    ．
    （1）求此重物在水平方向移动的距离BC；
    （2）求此重物在竖直方向移动的距离B′C（精确到0.1米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小刘同学在课外活动中观察吊车的工作过程，绘制了如图所示的平面图形．已知吊车吊臂的支点O距离地面的高OO′=2米．OA=10米，当吊臂顶端由A点抬升至A′点（吊臂长度不变）时，地面B处的重物（大小忽略不计）被吊至B′处，紧绷着的吊缆A′B′=AB．且cosA=
    3
    5
    ，sinA′=
    1
    2
    ．
    （1）求此重物在水平方向移动的距离及在竖直方向移动的距离；
    （2）若这台吊车工作时吊杆最大水平旋转角度为120°，吊杆与水平线的倾角可以从30°转到60°，求吊车工作时，工作人员不能站立的区域的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在10×10的网格纸上建立平面直角坐标系如图所示，在Rt△ABO中，∠OAB=90°，且点B的坐标为（3，4）．
    （1）分别画出△OAB关于y轴对称的△OA1B1与关于x轴对称的△OA2B2，并分别写出点B1，B2的坐标．
    （2）观察△OA1B1与△OA2B2，怎样由△OA1B1得到△OA2B2？

    查看答案和解析>>

    同步练习册答案