
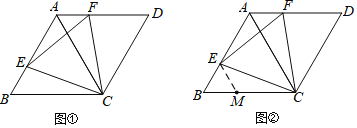
����Ŀ����ͼ��������ABCD�У���B= 60��.
��1����ͼ��.����E��F�ֱ��ڱ�AB��AD�ϣ���BE=AF����֤:��CEF�ǵȱ�������.
��2��С�����֣�����E��F�ֱ��ڱ�AB��AD�ϣ��ҡ�CEF=60��ʱ����CEFҲ�ǵȱ������Σ�
��ͨ����ͼ��֤�˲���;С��ͨ��̽������ΪӦ����CE= EFΪͻ�ƿڣ���������ȫ��������:Сٻ�ܵ�С����������������BC�Ͻ�ȡBM =BE��������ME����ͼ�ڣ��ܿ��֤������CEF�ǵȱ�������.�������Сٻ�ķ�����д��������֤������.
���𰸡���1������������2��������.
��������
��1����֤��BEC�ա�AFC�����ɵ�֤����2����֤�á�BEM�ǵȱ������Σ���֤��MEC��AFE������EC=EF�����ɡ�CEF=60������֤��.
��1����Ϊ�ı���ABCD�����Σ�����AB= BC=CD=AD.
��Ϊ��B=60�㣬���ԡ�ABC����ADC���ǵȱ�������.
����BC=AC����B=��CAF=��ACB=60�㣬
����ΪBE=AF������.��BEC�ա�AFC(SAS)������CE=CF����ECF=��BCA=60��
���ԡ�ECF�ǵȱ������Σ�
(2) ��ΪBE=BM����B= 60��
���ԡ�BEM�ǵȱ�������.
���ԡ�EMB=��BEM=60�㣬��EMC=��AEM=120��
��ΪAB= BC����EAF120�㣬����.AE=CM����EAF=��EM.
��Ϊ��FEC=60�㣬���ԡ�AEF+��CEM=60��.
����Ϊ��CEM+��ECM=60�����ԡ�AEF=��ECM.
������MEC��AFE(ASA)������EC=EF.
����Ϊ��FEC=60�㣬���ԡ�EFC�ǵȱ�������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����в�������һ�˻����������У���ÿ�ִ�Ⱦ��һ�˽�ƽ������x�ˣ�
��1�����һ�ֺ������������ú�x�Ĵ���ʽ��ʾ��
��2���ڽ���ڶ��ִ�Ⱦ֮ǰ������λ���߱���ʱ���벢�������ʵڶ��ִ�Ⱦ���ܹ��Ƿ����21�˻����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
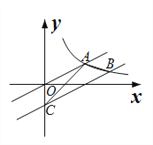
����Ŀ����ͼ����ֱ֪��![]() �뷴��������
�뷴��������![]() ��
��![]() ��ͼ���ڵ�A����ֱ������ƽ��4����λ��������������
��ͼ���ڵ�A����ֱ������ƽ��4����λ��������������![]() ��
��![]() ��ͼ���ڵ�B����y���ڵ�C������AB��AC������ABC�����Ϊ_______��
��ͼ���ڵ�B����y���ڵ�C������AB��AC������ABC�����Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
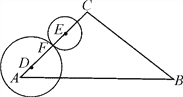
����Ŀ����ͼ������ABC�У���A=45�㣬AB=![]() ��AC=6����D��EΪ��AC�ϵĵ㣬AD=1��CE=2����FΪ�߶�DE��һ�㣨����D��E�غϣ����ֱ��Ե�D��EΪԲ�ģ�DF��EFΪ�뾶��Բ.����Բ���AB��BC������������ʱ���߶�DF���ȵ�ȡֵ��Χ��_______.
��AC=6����D��EΪ��AC�ϵĵ㣬AD=1��CE=2����FΪ�߶�DE��һ�㣨����D��E�غϣ����ֱ��Ե�D��EΪԲ�ģ�DF��EFΪ�뾶��Բ.����Բ���AB��BC������������ʱ���߶�DF���ȵ�ȡֵ��Χ��_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4��12�ջ�Ϊ�³����ͺ�Ϊ��P30��Pro�����ֻ����Ϻ��ٿ������ᣬij��Ϊ�ֻ�ר������ץס�̻�������10000̨��P30��Pro���ֻ��������ۣ�ÿ̨�ijɱ���4400Ԫ������ͬʱ����ڡ����ⷢ�ۣ���һ�����ڣ���������ÿ̨�ۼ���5400Ԫ��������100��Ԫ����������Ҳ�۳���ͬ�����ÿ��ֻ�����ÿ̨�ɱ�����400Ԫ����õ�����ȴ�ǹ��ڵ�6����
��1����õ����۸ÿΪ�ֻ���һ�������ڹ�����ۼ��Ƕ���Ԫ��
��2��������ó��սӰ�죬�ڶ������ڣ���������ÿ̨�ÿ��ֻ��ۼ��ڵ�һ�����ڵĻ����Ͻ���m%����������5m%����������ÿ̨�ۼ��ڵ�һ�����ڵĻ���������m%�������ڵڶ������ڽ�ʣ�µ��ֻ�ȫ�����꣬����ڶ������ڹ���������ܶ�ȹ��ڵ������ܶ��6993��Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У�E��BC��һ�㣬F��CD�ӳ�����һ�㣬![]() ������AE��AF��EF��GΪEF�е㣬����AG��DG��
������AE��AF��EF��GΪEF�е㣬����AG��DG��

��1����ͼ1����![]() ��
��![]() ����DG��
����DG��
��2����ͼ2���ӳ�GD��M��ʹ![]() ����M��MN��FD��AF���ӳ�����N������NG����
����M��MN��FD��AF���ӳ�����N������NG����![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
�÷�����ʷ���ƾã���˵���������������ʱ���ġ����顱���ý������ѧ���ŷ������������һ�����÷����������ɸ������һ����������������һ�С�һ�м��Խ����ϵ�����֮�Ͷ����.��ͼ1������һ�����÷�����1,2,3,4,5,6,7,8,9�Ÿ�������ɵ�һ���������еľ���(��ͼ)����Խ��ߡ����С�����ĺͶ�Ϊ15.
(1)̽�����о��������÷��м��������9�����ĺ���ȷ����������ϵ.������������������÷��м��������a����÷���9������֮���� ���ú�a����ĸ����ʽ��ʾ��
(2)Ӧ�ã�����ѡȡһ�����ݹ���һ�����÷������뵽��ͼ2��3��3�����У�ʹ��ÿ�С�ÿ�С�ÿ���Խ����ϵ�������֮�Ͷ�����21��


(3)��չ��
�������ɻ÷��ݻ���������һ������ͼ.������������1��3��5��7��9�����г�������ͼ3������ʮ�ֿ�������5������ʮ�ֿ��е�����֮���ܵ���2020�𣿲�˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ģ��μ�ʹ������ȫ�潨��С����ᵽ�˹�����ѽ�. Ϊ�˽�2017��ȫ��������֧���ݹ���ͳ�ƾ���֯ʵʩ��ס����֧������״�����飬�����ȷ�����������÷ֲ㡢��Ρ����˿ڹ�ģ��С�ɱ����ĸ��ʳ�����������ȫ��31��ʡ�������У���1650���أ��С����������ѡ16��������ͥ��Ϊ���黧����֪2017��ǰ�����Ⱦ����˾����ѿ�֧������ƽ������2016��ǰ�����Ⱦ����˾����ѿ�֧������ƽ������115%���˾�����֧��Ϊ11423Ԫ��������������ͳ��ͼ�ش����⣺�����¼������ս��������������

��1������ȵ��������������2017��ǰ�����Ⱦ����˾����ѿ�֧������ƽ������Ԫ����
��2������2017��ǰ�����Ⱦ����˾�����֧��������ҽ�Ʊ�����ռԲ�ĽǶ�����
��3������2017��ǰ�����Ⱦ����˾�����֧�������ھ�ס�Ľ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��b��cΪ��������a��0����ͼ��x����A����2��0���͵�B����y�Ḻ�����ڵ�C�������߶Գ���Ϊx=��![]() �����н����У�����Ľ����ǣ�������
�����н����У�����Ľ����ǣ�������
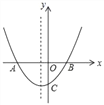
A. abc��0
B. ����ax2+bx+c=0�Ľ���x1=��2��x2=1
C. b2��4ac��0
D. a=b
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com