
 如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交
如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交 |
| AB |
 |
| AB |
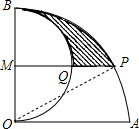 解:如图,连结OP.
解:如图,连结OP.| 90π×22 |
| 360 |
| 90π×12 |
| 360 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 30π×22 |
| 360 |
| π |
| 3 |
| 5π |
| 12 |
| ||
| 2 |


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
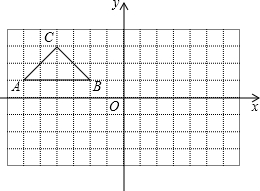 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:
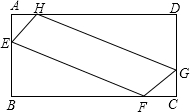 为了美化校园环境,某校准备在一块空地(如图所示的长方形ABCD,AB=10m,BC=20m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,那么在满足上述条件的所有设计中,是否存在一种设计,使得四边形EFGH的面积最大?
为了美化校园环境,某校准备在一块空地(如图所示的长方形ABCD,AB=10m,BC=20m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,那么在满足上述条件的所有设计中,是否存在一种设计,使得四边形EFGH的面积最大?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com