
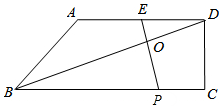
 已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.分析 (1)根据两角对应相等两三角形相似即可证明.
(2)①四边形ABPE是平行四边形,只要证明AE=BP即可.
②四边形ABPE是直角梯形,只要证明∠BPE=90°即可.
③四边形ABPE是等腰梯形,只要证明AB=PE即可.
解答 (1)证明:∵AE∥BC,
∴∠EDO=∠FBO,∠DEO=∠OFB,
∴△BOP∽△DOE.
(2)解:①如图1中,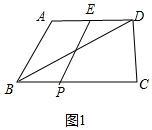
∵AE=ED,k=1,
∴AE=ED=BP,
∵AE∥PB,
∴四边形ABPE是平行四边形.
故答案为平行四边形.
②如图2中,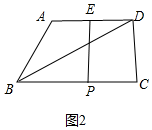
∵AE=DE,k=2,
∴PB=2ED=2AE,
∵AD:BC=2:3,
∴PC=DE,∵DE∥PC,
∴四边形CDEP是平行四边形,∵∠C=90°,
∴四边形CEEP是矩形,
∴∠EPB=∠EPC=90°,∵AE∥PB,AE≠PB,
∴四边形ABPE是直角梯形.
故答案为直角梯形.
③如图③中,作BM⊥AD于M.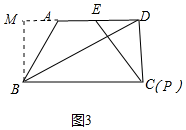
∵AE=DE,AD:BC=2:3,k=3,
∴PB=3DE,
∵BC=3DE,
∴点P与C重合,
∵∠M=∠BCD=∠BDM=90°,
∴四边形BCDM是矩形,
∴BM=DC,DM=BC,∵BC=3DE,AE=DE,
∴AM=DE,∵∠M=∠CDE=90°,
∴△ABM≌△ECD,
∴AB=EC,
∴四边形ABPE是等腰梯形.
故答案为等腰梯形.
点评 本题考查相似三角形的判定和性质、平行四边形的判定、直角梯形的判定.等腰梯形的判定等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-4,-6) | B. | (-4,-3) | C. | (-5,-2) | D. | (-5,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 加数的个数n | 和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-4) | B. | (-2,-3) | C. | (-2,-2) | D. | (-2,-5) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 165根、100个 | B. | 165根、55个 | C. | 135根、85个 | D. | 145根、100个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com