
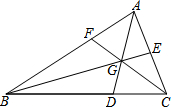
 已知:如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是60.
已知:如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是60. 分析 首先根据两个三角形的高相同时,面积的比等于它们的底边的比,求出S△CGD,S△CGE的大小,进而求出S△BCE的大小;然后根据三角形的中线将三角形分成面积相等的两部分,用S△BCE的面积乘以2,求出△ABC的面积是多少即可.
解答 解:∵BD=2DC,
∴S△CGD=$\frac{1}{2}$S△BGD=$\frac{1}{2}$×16=8;
∵E是AC的中点,
∴S△CGE=S△BGE=6,
∴S△BCE=S△BGD+S△CGD+S△CGE
=16+8+6
=30
∴△ABC的面积是:30×2=60.
故答案为:60.
点评 此题主要考查了三角形的面积的求法,以及三角形的中线的特征,要熟练掌握,解答此题的关键是要明确:(1)三角形的中线将三角形分成面积相等的两部分;(2)两个三角形的高相同时,面积的比等于它们的底边的比.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:| 乘车路程计价区段 | 0-10 | 11-15 | 16-20 | … |
| 对应票价(元) | 2 | 3 | 4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点C可能是线段AB的中点 | |
| B. | 点D一定不是线段AB的中点 | |
| C. | 点C,D可能同时在线段AB上 | |
| D. | 点C,D可能同时在线段AB的延长线上 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$,4 | B. | 2$\sqrt{10}$,4 | C. | 4,3$\sqrt{2}$ | D. | 6$\sqrt{2}$,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com