
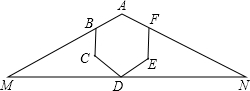
 如图,等腰三角形AMN中放置了一个正六边形,已知三角形AMN的面积是160平方厘米,那么正六边形ABCDEF的面积是60平方厘米.
如图,等腰三角形AMN中放置了一个正六边形,已知三角形AMN的面积是160平方厘米,那么正六边形ABCDEF的面积是60平方厘米. 分析 如图,连接AD、BE、CF,点O是正六边形的中心,是正六边形的边长为a.由S△AMN=160,可得方程$\frac{1}{2}$×$4\sqrt{3}$a×2a=160,求出a2,再根据S正六边形ABCDEF=6×$\frac{\sqrt{3}}{4}$×a2,即可解决问题.
解答 解:如图,连接AD、BE、CF,点O是正六边形的中心,是正六边形的边长为a.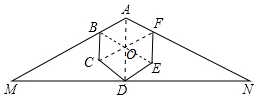
∵ABCDEF是正六边形,
∴∠DAB=∠DAN=60°,△ABO,△BCO,△DCO,△DEO,△EFO,△AOF都是等边三角形.
∵AM=AN,
∴AD⊥MN,
在RT△AMD中,∵∠ADM=90°,AD=2a,∠AMD=30°,
∴DM=2$\sqrt{3}$a,
∵S△AMN=160,
∴$\frac{1}{2}$×$4\sqrt{3}$a×2a=160,
∴a2=$\frac{40}{\sqrt{3}}$,
∴S正六边形ABCDEF=6×$\frac{\sqrt{3}}{4}$×a2=60.
故答案为60.
点评 本题考查正多边形与圆、等腰三角形的性质、直角三角形30度角的性质等知识,解题的关键是学会添加常用辅助线,学会利用参数,构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 所有的等腰三角形都是锐角三角形 | |
| B. | 等边三角形属于等腰三角形 | |
| C. | 不存在既是钝角三角形又是等腰三角形的三角形 | |
| D. | 一个三角形里有两个锐角,则一定是锐角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 、1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com