
【题目】已知关于x的方程kx2+(2k﹣1)x+k﹣1=0(1)只有整数根,且关于y的一元二次方程(k﹣1)y2﹣3y+m=0(2)有两个实数根y1和y2
(1)当k为整数时,确定k的值;
(2)在(1)的条件下,若m>﹣2,用关于m的代数式表示y12+y22.
【答案】(1)k=0,k=﹣1;(2)当m>﹣2时,y12+y22=(y1+y2)2﹣2y1y2=9+2m.
当m≥﹣![]() 时,有y12+y22=(y1+y2)2﹣2y1y2=
时,有y12+y22=(y1+y2)2﹣2y1y2=![]() +m.
+m.
【解析】
(1)要分两种情况讨论:
①k=0时,(1)方程为一元一次方程,可计算出此时方程的根是否为整数,若是,则k=0符合要求;
②k≠0时,(1)方程为一元二次方程,用因式分解法求出该方程的两个根,再根据这个方程只有整数根的特点,求出k的整数值,再根据的判别式将不合题意的k值舍去.
(2)将(1)得出的k值代入方程(2)中,首先根据根的判别式判断出m的范围,然后用根与系数的关系表示出所求的代数式的值.
解:(1)当k=0时,方程(1)化为﹣x﹣1=0,x=﹣1,方程有整数根
当k≠0时,方程(1)可化为(x+1)(kx+k﹣1)=0
解得x1=﹣1,x2=![]() =﹣1+
=﹣1+![]() ;
;
∵方程(1)的根是整数,所以k为整数的倒数.
∵k是整数
∴k=±1
此时△=(2k﹣1)2﹣4k(k﹣1)=1>0
但当k=1时,(k﹣1)y2﹣3y+m=0不是一元二次方程
∴k=1舍去
∴k=0,k=﹣1;
(2)当k=0时,方程(2)化为﹣y2﹣3y+m=0
∵方程(2)有两个实数根
∴△=9+4m≥0,即m≥﹣![]() ,又m>﹣2
,又m>﹣2
∴当m>﹣2时,y12+y22=(y1+y2)2﹣2y1y2=9+2m;
当k=﹣1时,方程(2)化为﹣2y2﹣3y+m=0,方程有两个实数根
∴△=9+8m≥0,即m≥﹣![]()
∵m>﹣2,
∴当﹣2<m<﹣![]() 时,方程(2)无实数根
时,方程(2)无实数根
当m≥﹣![]() 时,有y12+y22=(y1+y2)2﹣2y1y2=
时,有y12+y22=(y1+y2)2﹣2y1y2=![]() +m.
+m.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
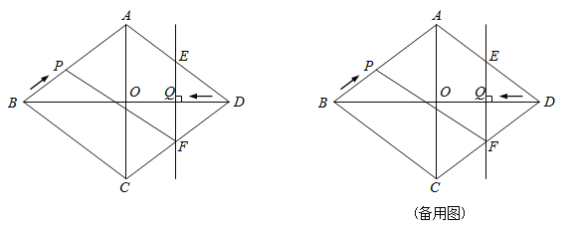
【题目】已知:如图,菱形ABCD中,对角线AC、BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE∶S菱形ABCD=17∶40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人打算用不锈钢条加工一个面积为0.8平方米的矩形模具.假设模具的长与宽分别为x米和y米.
(1)你能写出y与x之间的函数解析式吗?
(2)变量y与x是什么函数关系?
(3)已知这种不锈钢条每米6元,若想使模具的长比宽多1.6米,则加工这个模具共需花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假定甲、乙两人在一次赛跑中,路程S与时间T的关系在平面直角坐标系中如图所示,请结合图形和数据回答问题:
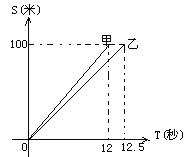
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)乙在这次赛跑中的速度为 ;
(4)甲到达终点时,乙离终点还有 米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com