
��֪����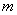 ��
��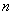 �Σ�ƽ������
�Σ�ƽ������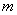 ��
��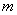 ��
��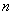 ��
��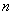 ��֮��ľ���ֱ�Ϊ
��֮��ľ���ֱ�Ϊ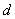 1��
1��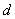 2��
2��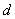 3����
3����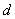 1 =
1 =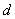 3 = 1��
3 = 1��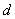 2 = 2 . ���ǰ��ĸ�����ֱ��ڡ�
2 = 2 . ���ǰ��ĸ�����ֱ��ڡ�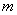 ��
��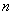 ��������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ�.
��������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ�.
��̽��1�� �� ��ͼ1��������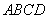 Ϊ�������ı��Ρ���
Ϊ�������ı��Ρ���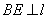 �ڵ�
�ڵ�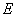 ,
,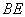 �ķ����ӳ��߽�ֱ���ڵ�
�ķ����ӳ��߽�ֱ���ڵ� . ��������
. �������� �ı߳�.
�ı߳�.
��̽��2�� �� ����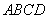 Ϊ�������ı��Ρ����䳤 ���� = 2 ��1 �������
Ϊ�������ı��Ρ����䳤 ���� = 2 ��1 �������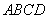 �Ŀ�Ϊ_____. (ֱ��д���������)
�Ŀ�Ϊ_____. (ֱ��д���������)
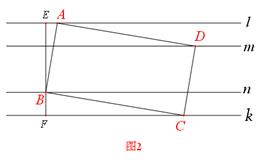
��̽��3�� �� ��ͼ2������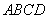 Ϊ�������ı��Ρ��ҡ�
Ϊ�������ı��Ρ��ҡ�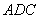 =60�㣬��
=60�㣬��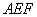 �ǵȱ������Σ�
�ǵȱ������Σ�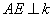 �ڵ�
�ڵ�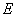 �� ��
�� ��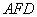 =90�㣬ֱ��
=90�㣬ֱ��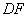 �ֱ�ֱ�ߡ��ڵ�
�ֱ�ֱ�ߡ��ڵ� ��
��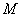 . ��֤��
. ��֤��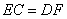 .
.
���� չ�� �� ��ͼ3���Σ��ȱ������� �Ķ���
�Ķ��� ��
��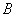 �ֱ�����ֱ�ߡ��ϣ�
�ֱ�����ֱ�ߡ��ϣ�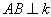 �ڵ�
�ڵ�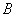 �� ��
�� ��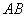 =4 ����
=4 ����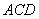 =90�㣬ֱ��
=90�㣬ֱ��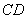 �ֱ�ֱ�ߡ��ڵ�
�ֱ�ֱ�ߡ��ڵ� ��
��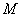 ����
����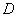 ��
��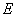 �ֱ����߶�
�ֱ����߶�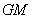 ��
��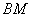 �ϵĶ��㣬��ʼ�ձ���
�ϵĶ��㣬��ʼ�ձ��� =
=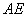 ��
��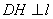 �ڵ�
�ڵ�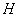 .
.
���룺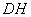 ��ʲô��Χ�ڣ�
��ʲô��Χ�ڣ�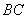 ��
��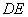 ����˵����ʱ
����˵����ʱ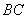 ��
��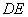 ������.
������.
 |


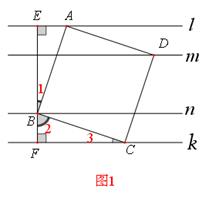 ������(1) ��ͼ1�� ��BE��l , l ��k ,
������(1) ��ͼ1�� ��BE��l , l ��k ,
���AEB=��BFC=90��,
���ı���ABCD�������Σ�
���1+��2=90�㣬AB=BC, �ߡ�2+��3=90��, �� ��1=��3,
��SABE�ըSBCF(AAS),
��AE=BF=1 , ��BE=d1+d2=3 , ��AB=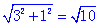 ,
,
 �������εı߳���
�������εı߳���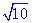 .
.
(2)��ͼ2,3���SABE�רSBCF,
��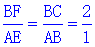 ��
��
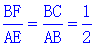
 ��BF=d3=1 ,
��BF=d3=1 ,
��AE=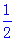 ��
��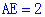
��AB=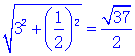 ��
��
AB=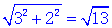
�����ABCD�Ŀ�Ϊ ��
��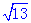 . (ע�⣺Ҫ��2��������ۣ�
. (ע�⣺Ҫ��2��������ۣ�
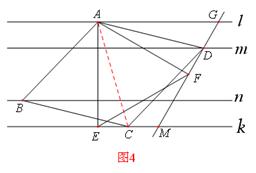 (3)��ͼ4������AC��
(3)��ͼ4������AC��
���ı���ABCD�����Σ�
��AD=DC,
�֡�ADC=60��,
��SADC�ǵȱ������Σ�
��AD=AC��
��AE��k , ��AFD=90��, ���AEC=��AFD=90�㣬
�ߨSAEF�ǵȱ������Σ� �� AF=AE,
��SAFD�ըSAEC(HL), ��EC=DF.
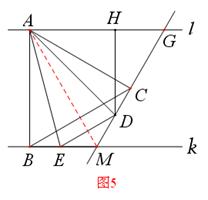 (4)��ͼ5����2��DH��4ʱ�� BC��DE .
(4)��ͼ5����2��DH��4ʱ�� BC��DE .
�������£�
����AM,
��AB��k , ��ACD=90��,
���ABE=��ACD=90��,
�ߨSABC�ǵȱ������Σ�
��AB=AC ,
��֪AE=AD, ��SABE�ըSACD(HL)����BE=CD��
��Rt�SABM��Rt�SACM��
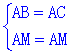 ����Rt�SABM��Rt�SACM(HL),
����Rt�SABM��Rt�SACM(HL),
�� BM=CM ��
��ME=MD,
��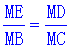 , ��ED��BC.
, ��ED��BC.





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��μ�ʱ��������ͬѧ����һ��������Ϸ������������д�����֩�1��0��1�Ŀ�Ƭ�����DZ�����ȫ��ͬ���������ſ�Ƭ���泯��ϴ�Ⱥ�����һ��ͬѧ�����ȡһ�ţ����������������Ϊp��ֵ��Ȼ��Ƭ�Żز�ϴ�ȣ���һ��ͬѧ�ٴ������ſ�Ƭ�������ȡһ�ţ����������������Ϊqֵ�����ν����Ϊ��p��q����
��1���������������״ͼ���б�����ʾ��p��q�����п��ܳ��ֵĽ����
��2�����������x�ķ���x2+px+q=0û��ʵ����ĸ��ʣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����x��һԪ���η��� 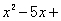 k=0����������ȵ�ʵ��������k��ȡ���������Ϊ_________.
k=0����������ȵ�ʵ��������k��ȡ���������Ϊ_________.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�龰��

�Ը���ͼ�е���Ϣ������������⣺
�� ����6�������� Ԫ������12�������� Ԫ.
�� С���С������2��������ʱС�췴����С����5Ԫ������Ϊ�����ֿ��������У������С�칺�������ĸ�������û�У���˵������.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м��������ǣ�������
| �� | A�� | a•a2=a3 | B�� | a2b��ab2=ab��a��b�� | C�� | 2m+3n=5mn | D�� | ��x2��3=x6 |


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��Բ�IJ����Ϊ15�У�������뾶Ϊ3�����Բ�ĸ�AOΪ��������
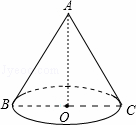
| �� | A�� | 3 | B�� | 4 | C�� | 5 | D�� | 15 |


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������������վλ�����������������뱱·����վ�ܽ������ԼΪ267000ƽ���ף���������267000�ÿ�ѧ��������ʾΪ  ( )
( )
��A��26.7��10 ��B��2.67��10
��B��2.67��10 ��C��2.67��10
��C��2.67��10 ��D��0.267��10
��D��0.267��10


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com