
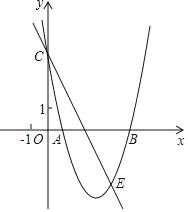
【题目】已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
(1)求抛物线的函数关系式;
(2)求抛物线的顶点坐标、对称轴;
(3)若过点C的直线与抛物线相交于点E(4,m),请连接CB,BE并求出△CBE的面积S的值.
【答案】(1)y=x2﹣6x+5;(2)当x≥3时y随x的增大而增大;(3)10.
【解析】
(1)设抛物线![]() 把C的坐标代入求出即可;
把C的坐标代入求出即可;
(2)把抛物线的解析式化成顶点式,求得对称轴,根据抛物线的性质即可求得x的取值;
(3)求出E的坐标,把C(0,5),E(4,-3)代入y=kx+b得到方程组,求出方程组的解即可得到一次函数的解析式,求出直线与X轴的交点,根据三角形的面积公式求出即可.
(1)∵A(1,0),B(5,0),
设抛物线![]()
把C(0,5)代入得:![]()
解得:a=1,
![]()
即抛物线的函数关系式是![]()
(2)![]()
∴抛物线的对称轴为x=3,
又∵二次函数![]() 的二次项系数为1>0,
的二次项系数为1>0,
∴抛物线的开口向上,
∴当x≥3时y随x的增大而增大;
(3)把x=4代入![]() 得:y=﹣3,
得:y=﹣3,
∴E(4,﹣3),
把C(0,5),E(4,﹣3)代入![]() 得:
得:![]() ,
,
解得:![]()
![]()
设直线![]() 交x轴于D,
交x轴于D,
当y=0时,![]() ,
,
∴x=![]() ,
,
∴OD=![]() ,
,
BD=5﹣![]() =
=![]() ,
,
![]()


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)若原方程的一根大于3,另一根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4, 1),B(-1,3),C(-1,1)
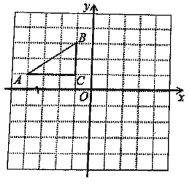
(1)将△ABC以原点O为旋转中心旋转180°,画出旋转后对应的△![]() ;平移△ABC,若A对应的点
;平移△ABC,若A对应的点![]() 坐标为(-4,-5),画出△
坐标为(-4,-5),画出△![]() ;
;
(2)若△![]() 绕某一点旋转可以得到△
绕某一点旋转可以得到△![]() ,直接写出旋转中心坐标是__________;
,直接写出旋转中心坐标是__________;
(3)在x轴上有一点P是的PA+PB的值最小,直接写出点P的坐标___________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
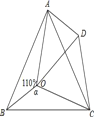
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,得△AOD,若△AOD为等腰三角形,则α=________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在图中正确作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 ,△A′B′C′的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com