
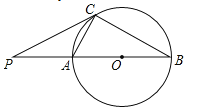
【题目】如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
【答案】(1)证明见试题解析;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
试题分析:(1)连接OC,由PC是⊙O的切线,得到∠1+∠PCA=90°,由AB是⊙O的直径,得到∠2+∠B=90°,从而得到结论;
(2)△ABQ与△ABC的面积相等时,有三种情况,即:①当∠AOQ=∠AOC=50°时;②当∠BOQ=∠AOC=50°时;③当∠BOQ=50°时,即∠AOQ=230°时;分别求得点Q所经过的弧长即可.
试题解析:(1)连接OC,∵PC是⊙O的切线,∴∠PCO=90°,∴∠1+∠PCA=90°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠2+∠B=90°,∵OC=OA,∴∠1=∠2,∴∠PCA=∠B;
(2)解:∵∠P=40°,∴∠AOC=50°,∵AB=12,∴AO=6,
①当∠AOQ=∠AOC=50°时,△ABQ与△ABC的面积相等,∴点Q所经过的弧长=![]() =
=![]() ;
;
②当∠BOQ=∠AOC=50°时,即∠AOQ=130°时,△ABQ与△ABC的面积相等,∴点Q所经过的弧长=![]() =
=![]() ;
;
③当∠BOQ=50°时,即∠AOQ=230°时,△ABQ与△ABC的面积相等,∴点Q所经过的弧长=![]() =
=![]() ;
;
综上所述,当△ABQ与△ABC的面积相等时,动点Q所经过的弧长为![]() 或
或![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
【题目】反比例反数y=![]() (x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=
(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=![]() (x>0)的图象于点C,连接BC、OC,S△BOC=3,则k= .
(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).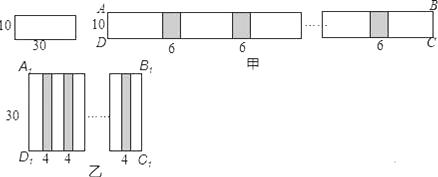
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上. 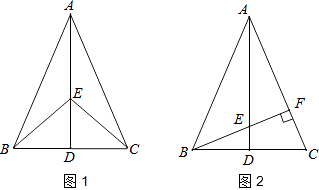
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
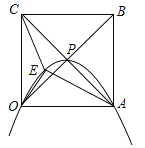
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系,①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
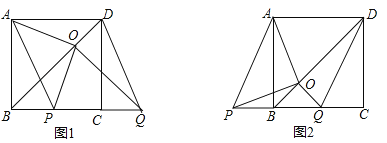
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
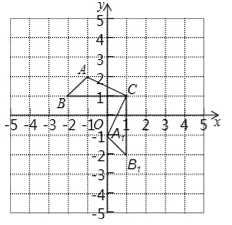
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请判断下列问题中,哪些是反比例函数,并说明你的依据.
(1)三角形的底边一定时,它的面积和这个底边上的高;
(2)梯形的面积一定时,它的中位线与高;
(3)当矩形的周长一定时,该矩形的长与宽.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com