
| A. | 调查某市中学生立定跳远的情况 | |
| B. | 调查某市市民对央视春晚的喜爱程度 | |
| C. | 调查某市市民的晨练情况 | |
| D. | 调查某班学生校服的尺寸 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 53 | B. | 126 | C. | 2015 | D. | 1892 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
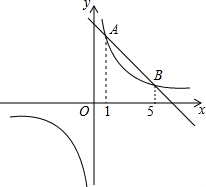 如图,直线y1=k1x-b,与双曲线y2=$\frac{{k}^{2}}{x}$交于A,B两点,它们的横坐标分别为1和5,则不等式k1x>$\frac{{k}^{2}}{x}$+b的解集为x<0或1<x<5.
如图,直线y1=k1x-b,与双曲线y2=$\frac{{k}^{2}}{x}$交于A,B两点,它们的横坐标分别为1和5,则不等式k1x>$\frac{{k}^{2}}{x}$+b的解集为x<0或1<x<5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
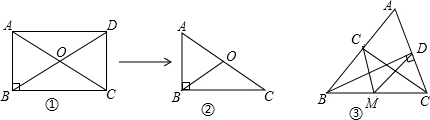
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
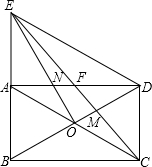 如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.
如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).
如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
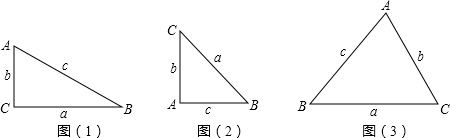 发现问题:
发现问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}>\frac{1}{2}-\frac{2}{3}①}\\{2x≥3x-1②}\end{array}\right.$请结合填题意空,完成本题的解答
解不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}>\frac{1}{2}-\frac{2}{3}①}\\{2x≥3x-1②}\end{array}\right.$请结合填题意空,完成本题的解答查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com